Формализация описательной части задачи

Пример задачи.

Дано: предприятие, которое производит 2 вида продукции в 3 цехах: А, Б, В, в каждом из цехов установлено соответственно 24, 15, 8 ед. оборудования. Нормы использования оборудования за 1 час/ед. продукции представлена в таблице

Цех	Вид продукции
1 вид	2 вид
А	2 м/ч	3 м/ч
Б	1 м/ч	3 м/ч
В	-	2 м/ч

Прибыль от 1 вида продукции 1 рубль, 2 вида – 2 рубля.

Требуется определить объем выпуска продукции 1 и 2 вида, приносящий максимум прибыли?

Составление модели:

Пусть

	- Искомый объем продукции первого вида   - объём продукции второго вида

Цель максимум прибыли.

1 руб.* X1 – прибыль от реализации 1 вида продукции

2 руб.* X2 - прибыль от реализации 2 вида продукции

Целевая функция

Обозначим в целевой функции коэффициенты при переменных через С1 и С2, тогда целевая функция будет иметь вид:

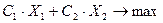
Введем систему ограничений, которая характеризует использование оборудования. Планирование использования машин по цехам не должен превышать наличие этого оборудования по цеху А (из таблицы).

	- Ограничение первое по цеху А - Ограничение второе по цеху Б - Ограничение третье по цеху В   - Общие ограничения

Решение задачи возможно двумя методами графоаналитическим и симплексным.

2. Представим решение задачи графоаналитическим методом. С этой целью используем изложенные выше правила и построим координатную плоскость.

9

8 (1)

6

4 А В (3)

2 С

1 (2)

О 1 2 3 4 5 6 7 8 9 10 11 Д 12 13 14 15 16

Фигура получилась от пересечения линейных форм. Многоугольник определяет ОДР, с целью нахождения вершины (значения наилучшей альтернативы). Введем дополнительный уровень, произвольно, находящийся в ОДР.

К графическому методу решения задачи выбора из совокупности альтернатив наилучшей, всегда можно свести к решению двухмерной задачи графическим способом.

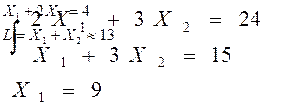Аналитический способ нахождения координаты точки С., используется при отсутствии необходимости графического представления оптимального решения. В этом способе система уравнений (применимо к ранее формулированной задачи) будет иметь вид:

Поставим полученные решения в уравнение 2, имеем

получим:

X2=2

9+3Х2 = 15

Задача оптимизации доходов.

Завод изготавливает детали для автомобиля. Выпуск второго типа деталей (X1,X2). Завод располагает фондом рабочего времени 4000 ч/ч в неделю. Для производства одной детали типа X1 требуется 1 ч/ч, и для X2 2ч/ч. Производственная мощность завода позволяет выпускать X=2250 и X=1550 деталей в неделю. Каждая деталь типа X2 требуют 2 кг металлических стержней, и 5 кг листового метала. Для производства X1 (1 деталь) необходимо 5 кг стержней и 2 кг листового металла. Уровень запаса каждого вида металла составляет 10000кг. Ежедневно завод поставляет 600 деталей 1 вида своему заказчику.

Существует также профсоюзное соглашение в соответствие, с которым общее число производимых в неделю деталей составляет не менее 1500штук.

Требуется определить сколько деталей каждого типа нужно производить, чтобы максимизировать общий доход за неделю, если доход за неделю X1=30 у.е., X2=40 у.е.?

Критерий максимум доход, целевая функция имеет вид:

- План производства 1 детали (объем производства)   - План производства 2 детали

Формализация задачи: пусть переменная

Тогда целевая функция будет иметь вид:

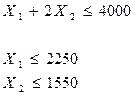
введем ограничения:

	1) ограничение по фонду рабочего времени, планированное рабочее время не должно иметь ограничение 2) по производственной мощности     3) по уровню запасов, планированное использование материалов каждого вида не должно превышать 10000 кг   4) по обязательствам поставки первых деталей 5) по профсоюзному ограничению 6) условие не отрицательности

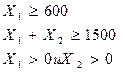
Решение:

Строим систему координат, при фиксированном времени.

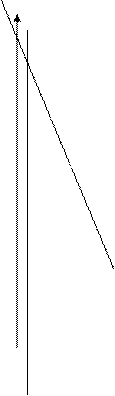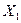5

4

(2)

2 С д

1 Д

1 2 3 4 5 6 7 8

Построение областей ограничения

Строим целевую функцию (произвольно)

Оптимальная точка определения плана производства достигается максимальным доходом.

Это точка Д (1500, 1250)

Аналитический способ:

Резюме

Рассмотренный выше задачи оптимизации планирования производства по критерию максимум прибыли и дохода, при решения графическим или аналитическим методом, в случаи небольшой размерности переменных наглядны и точны в своих решениях.

Дата добавления: 2014-01-13