
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейное программирование и симплексный метод выбора
|
|
|
|
Лекция10.
наилучших решений в задачах планирования производства.
Классическая постановка задачи линейного программирования.
Дано: система математически- линейных зависимых уравнений с неизвестными
|

называемая система ограничений задачи линейного программирования, имеющая вид:

где
|

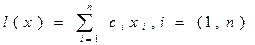
это выражение 9.2 принято называть линейной формой, которая часто отображается в виде:
 |

выражение 9.1-9.3 можно отобразить в более компактной форме, в виде матрицы, тогда линейная форма будет иметь вид:
AX=B 9.4
L=CX 9.5
При B>0, X>0, L—max(min)
Выражение 9.4 матрица А имеет размерность n*m, x*c
Матрица В - m - мерный вектор столбец
Матрица Х - n - мерная вектор строка
Матрица С – n - мерная вектор строка
Если из n вычисть m и полученное значение с этим индексом, предположить их равным 0, то мы получим базисное решение. Базисное решение в линейном программировании называется допустимым, если базисные переменные не отрицательны по значению.
Решением системы уравнения 9.4 в условиях полной информатизации может быть получена различными способами. Наиболее простым способом 9.1-9.4 является симплексный метод. Основой всех методов получения решения уравнения ЛП в том числе и симплексный, является итерационный процедуры. Основной итерационной процедуры является введение наряду с базисными переменными независимых и ограниченных переменных (свободных). Из которых в условиях ограничения получаются отправные решения доставляющие целевой функции начальные значения, затем путем замены свободных переменных на базисные, составляются улучшенные значения целевой функции.
Если целевая функция L(x) стремится к max в задачи максимизации, то в ее индексной строке не должно быть не одного отрицательного числа и в этом случаи значение L(x) будет оптимальным, т.е. иметь максимум.
Если L(x) стремится к min, т.е. решается задача минимизации, то в ее индексной строке не должны быть положительные числа именно это значение будет оптимальным.
Рассмотрим изложенное выше положение на примере решения задачи №1, в лекции 8,
в которой имеет место следущая формализованная запись в канонической форме:
|
 |
Для решения уравнения 9.6 симплексным методом необходимо перевести целевую функцию:
|

Для решения введем дополнительные переменные в каждое уравнение соответственно, тогда система 9.6 будет иметь вид:
 |
все переменные должны быть введены и в целевую функцию, тогда
|
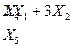
- А, - В, -С
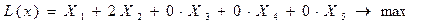
Дополнительные переменные прибыли не дают, поэтому в целевой функции они будут равны нулю, с учетом этого целевая функция будет иметь вид:

Каждая из дополнительных или базисных переменных входит только в одно уравнение. Все они входят с коэффициентом +1. Свободные переменные на первом итерационном шаге приравниваются к нулю:
Для получения второго решения в симплексном методе составляется отправная таблица, имеющая вид:
| С/б | Х/б | В | |||||
| Х1 | Х2 | Х3 | Х4 | Х5 | |||
| X3 | |||||||
 0 0
| X4 | ||||||
| X5 | |||||||
| Zj-Cj | Z0=0 | -1 | -2 |
Примечание: здесь и далее элипс – обозначает генеральный элемент
В отправной таблице введены следующие обозначения:
С/б - коэффициенты при базисных переменных целевой функции
Х/Б – базисные переменные
В – столбец свободных членов
|

|

|
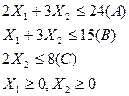 |
Нижние строки определяют разницу между
 |
Алгоритм определения оптимального решения:
исходя из выше изложенной теории данные, полученные в симплексной таблице или в таблице вообще при максимизации целевой функции, решение будет оптимальным, если в индексной строке не будет отрицательных чисел
при минимизации целевой функции, решение будет оптимальным, если в индексной строке не будет положительных чисел (это так называемая двойственная задача линейного программирования)
Правила составления 1-ой итерационной таблицы по отправной
1. наибольшая по абсолютным значениям переменная, в индексной строке отправной таблице, указывает на новую базисную переменную, подлежащую замене
2. определение старой базисной переменной, которая должна в новом решении уступить место новой базисной величине, выбирается путем деления свободных членов столбца В на Х2
24/3=8,
15/3=5,
8/2=4.
Найденные отношения определяют переменные старого значения, которые должны уступить место новой переменной, оно должно быть минимальным, т.е. Х2 заменяется на Х5
Столбец новой базисной переменной называется ключевым столбцом. Строка, куда попадают новые переменные, называется ключевой строкой.
На пересечении ключевой строки и ключевого столбца стоит генеральный элемент.
Составляем i=2 симплексную таблицу:
| С/б | Х/б | В | |||||
| Х1 | Х2 | Х3 | Х4 | Х5 | |||
| X3 | -3/2 | ||||||
| X4 | -3/2 | ||||||
| X2 | ½ | ||||||
| Zj-Cj | Z=8 | -1 |
Правила составления i-ой текущей итерационной таблицы: i = (1,n)
1. старый ключевой столбец переписывают в новую таблицу в виде нулей кроме элементов стоящих на перемещении столбца и ключевой строки
2. элементы новой строки соответствуют старой ключевой строки, она находится путем деления
элементов старой ключевой строки на генеральный элемент.
при формировании базисной строки вместо Х5--------Х2
3. столбцы старой таблицы, содержащие в ключевой строке «0», переписываются в новую таблицу без изменения
4. все остальные элементы новой таблицы определяются по формуле:
новый = старый (минус) элемент ключ строки * элемент ключ столбца
лемент элемент генеральный элемент
пример
24 - 8*3/2=12
15 - 8*3/2=3
0 - 1*3/2=-3/2
Решение не оптимально (8 рублей прибыли на ед. продукции), т.к. имеется в индексной строке отрицательное значение. По второй итерации выпуск продукции 2 вида в количестве 4 ед. за час, при этом, предыдущий получает прибыль 8 рублей в час, и остаются, не использованы машины в цехе
А-12, в цехе В-3.
Используя выше изложенные правила, проводим следующее итерационное решение. Составляем новую таблицу, выделив в таблице 2 ключевой столбец и ключевую строку, получив генеральный элемент на их пересечении. Пользуясь правилами, заполняем таблицу i= 3:
 С/б С/б
| Х/б | В | |||||
| Х1 | Х2 | Х3 | Х4 | Х5 | |||
| Х3 | -2 | 3/2 | |||||
| Х1 | -3/2 | ||||||
| Х2 | 1/2 | ||||||
| Zj-Cj | Z0=11 | -1/2 |
12-3*2/1=6
4-0*3/1=4
0-1*2/1=-2
-3/2-(-3/2*2)/1=3/2
т.к. в индексной строке имеется отрицательное значение, то решение не является оптимальным и целевая функция не отражает максимум прибыли (11 рублей). Введем еще одну итерацию В таблице 3 определяем ключевую строку и ключевой столбец и, используя правила1-4., составляем i=4 таблицу.
| С/б | Х/б | В | |||||
| Х1 | Х2 | Х3 | Х4 | Х5 | |||
| Х5 | 2/3 | -4/3 | |||||
| Х1 | -1 | ||||||
| Х2 | -1/3 | 2/3 | |||||
| Zj-Cj | Z0=13 | 1/3 | 1/3 |
В индексной строке отсутствуют отрицательные значения, следовательно это и есть оптимальное решение, максимум прибыли составляет 13 рублей.
Лекция 11. “Двойственная задача в линейном программировании.”
На практике часто приходится сталкиваться с задачами планирования при условии минимизации целевой функции. Такого рода задачи обычно связаны не с получением максимальных доходов или прибыли, а с получением минимальных затрат, необходимых для решения производственных задач, приносящих максимальную прибыль.
В качестве примера рассмотрим первую задачу оптимизации плана производства, в которой выпускается 2 вида продукции в цехах А, Б и В, оснащенных оборудованием в следующих количествах:
| А | ||
| Б | ||
| В | - |


 - объем выпуска продукции первого и второго вида соответственно.
- объем выпуска продукции первого и второго вида соответственно.
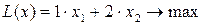 (прибыль)
(прибыль)
 шт/час
шт/час 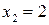 шт/час
шт/час  р/час
р/час
Примечание:
В двойственной задаче, если ограничения имеют знак ≥, то для выравнивания левой и правой части ограничения, вводится базисная переменная со знаком “+”, если ограничения имеют знак ≤, то вводится базисная переменная со знаком “-“, например:

Примечание:
Если “5” – минимально допустимый результат, то 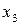 - величина превышения этого результата.
- величина превышения этого результата.
Если независимые переменные вводятся со знаком “+”, то они показывают количество неиспользуемых ресурсов (см. лекцию 10).
Если базисная переменная вводится со знаком “-“, то она показывает избыток продукции при постоянстве ресурсов.
Применительно к 1-ой задаче, в рамках её двойственности, можно потребовать рассмотрение задачи аренды оборудования, необходимого для выпуска продукции 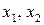 и минимизировать общую плату за арендное оборудование. В этом случае формализация задачи минимизации арендной платы оборудования при производстве продукции вида
и минимизировать общую плату за арендное оборудование. В этом случае формализация задачи минимизации арендной платы оборудования при производстве продукции вида 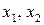 будет иметь вид:
будет иметь вид:
Пусть  - аренда 2-х маш/час на ед. продукции вида 1 оборудования цеха А.
- аренда 2-х маш/час на ед. продукции вида 1 оборудования цеха А.
В цехе А – 24 станка.
 - арендная плата за 1 час использования станка цеха Б.
- арендная плата за 1 час использования станка цеха Б.
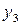 - арендная плата за 1 час использования станка цеха В.
- арендная плата за 1 час использования станка цеха В.
При выпуске единицы продукции первого вида, по условию задачи из таблички надо использовать 2 маш/часа оборудования цеха А и одного машиночаса оборудования цеха Б, при этом получается прибыль при производстве 1-го вида продукции – 1 руб. Для второго
вида продукции, по аналогии, прибыль – 2 руб. Требуется минимизировать арендную плату за оборудование при производстве 2-х видов продукции.
При введенных обозначениях имеем:
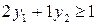 (плата за аренду должна быть менее 1 руб.)
(плата за аренду должна быть менее 1 руб.)

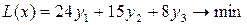
Выбор оптимальных вариантов решения:
1) Приводим систему уравнения к канонической форме:


Сведем решение к симплексному методу:
| Сб | Уб | В | М | М | |||||
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | |||
| М | y6 | -1 | |||||||
| М | y7 | -1 | |||||||
| Zj-Cj | 3 M | 5 M -24 | 4 M -15 | 2 M -8 | - M | - M |
Переход от отправной таблицы к следующей производится в соответствии с правилами симплексного метода (лекция 10).
В соответствии с чем, ключевым столбцом будет 4-ый, ключевой строкой будет 1-ая, на их пересечении – генеральный элемент.
Используя 4 правила из лекции 10, составим 2-ую таблицу:
| Сб | Уб | В | М | М | |||||
| y1 | y2 | y3 | y4 | y5 | y6 | y7 | |||
| М | y1 | 0,5 | 0,5 | -0,5 | 0,5 | ||||
| М | y7 | 0,5 | 1,5 | 1,5 | -1 | -1,5 | |||
| Zj-Cj | 0,5 M -12 | 1,5 M -3 | 2 M -8 | 1,5 M -12 | - M | -2,5 М +12 |
Примечание:
В двойственной задаче, коэффициент при базисной переменной принимается, как большое число, условно равное М, превышающее по своему значению максимальный коэффициент при независимой переменной целевой функции.
Дальнейшие итерационные процедуры проводятся до исчезновения в индексной строке положительных чисел, оптимальным для ЛПР будут значения затрат по арендной плате без наличия в индексной строке отрицательных чисел.
Лекция 12. Нелинейное программирование в задачах
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 304; Нарушение авторских прав?; Мы поможем в написании вашей работы!