Распределения разнородных ресурсов

Нелинейное программирование (НП) – это математические методы определения max или min целевой функции при наличии ограничений в виде неравенств или уравнений.

Целевая функция или хотя бы одно из ограничений – нелинейное.

Смысл решения задач НП заключается в определении условий, обращающих ЦФ в экстремум.

Нелинейное программирование НП – это метод выбора наилучшего плана распределения неоднородных ресурсов, доставляющий в экстремум ЦФ.

Методом НП решаются задачи распределения неоднородных ресурсов при следующей формулировке её в общем виде.

Пусть имеется m разнородных ресурсов, которое предполагается распределить по n потребителям.

Известны либо оценочные, либо вероятностные возможности переработки i-ого ресурса j-ым потребителем, а так же эффективность использования Э_ij

Распределение ресурсов по потребителям характеризуется параметром управления

, где 0 – если i-ый ресурс не направляется j-ому потребителю, а 1 –наоборот

требуется распределит ресурсы по потребителям так (т.е. выбрать такие значения U_ij), что бы величина:

1. суммарной эффективности использования всех видов ресурсов была max.
2. что бы величина полной вероятности достижения целевой функции была max.

Рассмотрим первый случай.

Для него (12.1)

Где x_ij –кол-во ресурсов i-ого типа, назначенные j-ому потребителю при ограничения 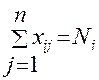(12.2)

Где N_i – кол-во единиц ресурса i-ого вида

Задача

Даны 2 группы разнородных ресурсов (m=2), которые можно включить в 3 проекта (n=3)

В первой группе ресурсов 6 единиц (N₁=6); во второй группе – 10 ед. (N₂=10).

Оценки важности проектов заданы таблицей.

Проекты
Pj – оценка	0,3	0,2	0,5

Эффективность вложений ресурсов различного рода Э_ij задана в таблице

Номер групп ресурсов	Номера проектов
	0,4	0,1	0,5
	0,2	0,4	0,2

Распределение ресурсов по проектам характеризуется исходной матрицей

А = ||X_ij||

Требуется распределить разнородные ресурсы так по проектам, чтобы Э_Σ=max

Решение выполняется итерационным процессом

Алгоритм решения:

1. В области изменения максимизирующей функции определяется исходная отправное допустимое решение Э_ij удовлетворяющая ограничительные условия задачи.
2. с помощью специального Е критерия проверяется достаточно ли близко полученное решение к оптимальному (жилаемому).
3. если полученное отклонение 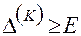, то путём построения, так называемого, возможного направления и определения в этом направлении конечного шага приближения к оптимуму, получают новое допустимое решение, которое увеличиное значение макс.функции.
4. процесс расчётов носит характер итерации, на котором до полученного решения с максимальным откланением (min^(K)>Δ).

это и будет решение близкое с заданной точностью приближения Е.

реализация расчётов по алгоритму.

1. определяется отправное допустимое решение А⁽⁰⁾=||x_ij⁰||

где, А⁰ – матрица, характеризующая отправное распределение ресурсов по проектам.

Примечание: в качестве отправного распределения может быть взято любое (и произвольное в том числе) распределение с ограничительным условием задачи.

Чем отправное распределение ближе к оптимальному, тем меньше итераций понадобится.

Берём произвольно

Столбцы – номера проектов

Строки – номера видов ресурсов

Далее осуществляется итерационная процедура. В результате выполнения к – итераций, получается К-ое приближение к оптимальному.

1. Определяется компонента матрицы возможного направления итерационных шагов, имеющая вид:

S^(K)=||S_ij^(K)||, где S_ij^(K)=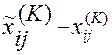

Величина находится с помощью матрицы y_ij^(K).

Резюме: при заданном Е критерии 0,01 необходимо после шага 4 итерации. В которых Δ^(K) больше Е кроме 4-ой итерации.

Точность приближения к оптимуму определяются ЛПР и Е может ровняться и 0,02; и 0,01; и 0,1; и 0,2.

Примечание: в курсовых работах точность должна быть не менее 0,1.

Лекция 13. Вероятностные методы принятия решений в задачах оптимизации закупок

Вероятность какого-либо события – это отношение количества исходов (m) в опытах к общему количеству опытов (n).

P = m/n 13.1.

Априорная вероятность (доопытная) – вероятность события до проведения эксперимента.

Апостериорная вероятность (послеопытная) - вероятность наступления события в конце эксперимента.

Безусловная вероятность – вероятность наступления события, не связанного в опыте ни с каким другим событием. ().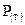

Условная вероятность – вероятность события T при условии, что произошло событие S. ().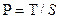

Формула полной вероятности:

(13.2),
где: 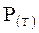- безусловная вероятность события T;
- условная вероятность того, что событие Т наступит при наступлении события ;
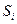- априорная вероятность события .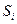

Формула Байеса:

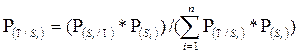(13.3)

Пример. Прогноз погоды на 12 июня показал, что день будет солнечным (событие ). Этот прогноз может быть ошибочным с условными вероятностями P(/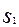)=0.9 и P(/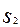)=0.3; апостериорные вероятности событий: 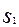- солнце, 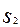- дождь; априорные вероятности: P(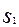)=0,8, P(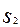)=0,2. тогда по формуле Байеса найдем апостериорные вероятности:

P=(0.9*0.8)/(0.9*0.8)+(0.3*0.2)=0.923 – вероятность солнца;

P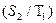=1-0.923=0.0769 – вероятность, что пойдет дождь.
При решении задач, содержащих случайные события, необходимо иметь статистику наступления этих событий. Этой статистикой менеджер располагает практически всегда. Используя такую статистику, менеджер может с успехом решать задачи, в которых имеется зависимость конечного результата от случайного спроса.

Обычно такой класс задач подразумевает наличие трех видов критериев в принятии решений:

1. max-max (т.е. максимальный из максимумов);

2. min-max (минимальный из максимумов);

3. max-min (максимальный из минимумов).

Используя такого плана критериев, можно оперировать при решении задач оптимизации закупок, оптимизации создания резерва запасов и других аналогичных задач. Можно использовать как вероятностный подход, так и без учета вероятности.

При вероятностном подходе часто используется статистическая средняя математического ожидания, имеющая вид:

(13.4).

Пример. Определить среднюю длину куска ткани, если результаты замеров представлены в таблице:

длина							n
частота
m
P=m/n	0.05	0.15	0.6	0.1	0.08	0.02

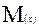= (42*0,05)+(41*0,15)+(40*0,6)+(39*0,1)+(38*0,08)+(37*0,02)=40,5м

Дата добавления: 2014-01-13