
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перетворювачі кодів, шифратори та дешифратори
|
|
|
|
| Таблиця 10.1 |
Для уявлення інформації використовуються різноманітні двійкові і двійково-десяткові коди: прямий, обернений, додатковий, “з надлишком 3” та інші. Тому у цифрових системах широко застосовуються перетворювачі кодів, забезпечуючі перетворення інформації з однієї форми у іншу.
| a3 | a2 | a1 | a0 | b3 | b2 | b1 | b0 |





 Найпростішу структуру має перетворювач чисел з прямого коду А = аk … а1а0 у обернений В = bk … b1b0, що згідно із значенням знакового розряду Z або зберігає значення цифри кожного розряду (при Z = 0 bi = аi, i = 0, …, k), або змінює на протилежне значення (при Z = 1 bi = аi, i = 0, …, k). Логічна функція, визначаюча значення і-го розряду має вигляд bi = Zаi Zаi і реалізується схемою Виключаюче АБО.
Найпростішу структуру має перетворювач чисел з прямого коду А = аk … а1а0 у обернений В = bk … b1b0, що згідно із значенням знакового розряду Z або зберігає значення цифри кожного розряду (при Z = 0 bi = аi, i = 0, …, k), або змінює на протилежне значення (при Z = 1 bi = аi, i = 0, …, k). Логічна функція, визначаюча значення і-го розряду має вигляд bi = Zаi Zаi і реалізується схемою Виключаюче АБО.

 Логічні схеми перетворювачів кодів можна отримати, користуючись наведеною раніше методикою. Наприклад, для чотирьохрозрядного перетворювача від’ємного числа з прямого коду у додатковий таблиця істиності має вигляд табл.10.1.
Логічні схеми перетворювачів кодів можна отримати, користуючись наведеною раніше методикою. Наприклад, для чотирьохрозрядного перетворювача від’ємного числа з прямого коду у додатковий таблиця істиності має вигляд табл.10.1.
Відповідні карти Карно показані на мал.10.2 (b0 = a0).
З наведених карт Карно отримуємо:


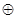








 b3 = a0a3 a1a3 a2a3 a0a1a2a3 = (a0 a1 a2) a3;
b3 = a0a3 a1a3 a2a3 a0a1a2a3 = (a0 a1 a2) a3;
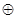






 b2 = a0a2 a1a2 a0a1a2 = (a0 a1) a2;
b2 = a0a2 a1a2 a0a1a2 = (a0 a1) a2;
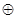


 b1 = a0a1 a0a1 = a0 a1;
b1 = a0a1 a0a1 = a0 a1;
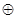 b0 = a0 = a0 0;
b0 = a0 = a0 0;
b3 b2 b1









 a0 a0 a0
a0 a0 a0




 a2 1 1 1 1 0 0 0 1 1 0 1 0
a2 1 1 1 1 0 0 0 1 1 0 1 0


 0 0 0 0 a3 0 0 0 1 1 0 1 0
0 0 0 0 a3 0 0 0 1 1 0 1 0


 0 0 0 1 1 1 1 0 1 0 1 0
0 0 0 1 1 1 1 0 1 0 1 0






 1 1 1 0 1 1 1 0 1 0 1 0
1 1 1 0 1 1 1 0 1 0 1 0
a1 a1 a1
Мал.10.2. Карти Карно функцій b3, b2, b1 перетворювача
прямого коду у додатковий.
У загальному випадку значення і-го розряду визначається виразом:



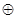 bі = (a0 a1 … aі-1) aі.
bі = (a0 a1 … aі-1) aі.
   a0 b0 a0 b0
Мал.10.3. Перетворювач кодів. |
Використовуючи елементи АБО та Нерівнозначність, отримуємо схему, показану на мал.10.3. Із збільшенням номеру розряду вихідна функція перетворювача суттєво ускладнюється. Тому для перетворення багаторозрядних чисел доцільно застосовувати схеми перетворення у обернений код, а потім додавати одиницю для отримання додаткового, використовуючи суматор (схему для додавання чисел).

 Серед найпоширеніших видів перетворення інформації можна виділити шифрацію і дешифрацію. Шифрацією називається перетворення m-розрядного двійкового коду, маючого km байдужих наборів вхідних змінних, у n-розрядний код, маючий меншу кількість розрядів (n < m) і байдужих наборів (kn < km). При цьому між вхідними і вихідними робочими наборами встановлюється взаємно однозначна відповідність. У результаті шифрації здійснюється “стискування” інформації для передавання її меншою кількостю ліній. Зворотнє перетворення називається дешифрацією. Функціональні вузли для виконання цих операцій називаються шифраторами і дешифраторами. Вони відрізняються за кількістю входів і виходів і називаються “шифратор (дешифратор) з m у n”. Максимальна кількість входів шифратора не перебільшує кількості можливих комбінацій вихідних сигналів: m 2n, а кількість виходів дешифратора задовольняє умові n 2m.
Серед найпоширеніших видів перетворення інформації можна виділити шифрацію і дешифрацію. Шифрацією називається перетворення m-розрядного двійкового коду, маючого km байдужих наборів вхідних змінних, у n-розрядний код, маючий меншу кількість розрядів (n < m) і байдужих наборів (kn < km). При цьому між вхідними і вихідними робочими наборами встановлюється взаємно однозначна відповідність. У результаті шифрації здійснюється “стискування” інформації для передавання її меншою кількостю ліній. Зворотнє перетворення називається дешифрацією. Функціональні вузли для виконання цих операцій називаються шифраторами і дешифраторами. Вони відрізняються за кількістю входів і виходів і називаються “шифратор (дешифратор) з m у n”. Максимальна кількість входів шифратора не перебільшує кількості можливих комбінацій вихідних сигналів: m 2n, а кількість виходів дешифратора задовольняє умові n 2m.

 Шифратори використовуються для передавання інформації між різними пристроями при обмеженій кількості ліній зв’язку, а також перетворення уведених з клавіатури чисел у двійкову форму.
Шифратори використовуються для передавання інформації між різними пристроями при обмеженій кількості ліній зв’язку, а також перетворення уведених з клавіатури чисел у двійкову форму.

 Дешифратор що реалізує на виходах усі мінтерми вхідних змінних (n = 2m) або інверсії мінтермів (макстерми) називається повним. Логічний вираз для і-ї вихідної функції повного дешифратора має вигляд Fi = m i = M i або Fi = Mi = m i. Так, повний дешифратор “з 3 у 8”, реалізуючий макстерми трьох змінних, має такі вихідні функції:
Дешифратор що реалізує на виходах усі мінтерми вхідних змінних (n = 2m) або інверсії мінтермів (макстерми) називається повним. Логічний вираз для і-ї вихідної функції повного дешифратора має вигляд Fi = m i = M i або Fi = Mi = m i. Так, повний дешифратор “з 3 у 8”, реалізуючий макстерми трьох змінних, має такі вихідні функції:







 F0 = x1 x2 x3 = M0 = m0 = x1 x2 x3,
F0 = x1 x2 x3 = M0 = m0 = x1 x2 x3,






 F1 = x1 x2 x3 = M1 = m1 = x1 x2 x3,
F1 = x1 x2 x3 = M1 = m1 = x1 x2 x3,






 F2 = x1 x2 x3 = M2 = m2 = x1 x2 x3,
F2 = x1 x2 x3 = M2 = m2 = x1 x2 x3,






 F3 = x1 x2 x3 = M3 = m3 = x1 x2 x3,
F3 = x1 x2 x3 = M3 = m3 = x1 x2 x3,





 F4 = x1 x2 x3 = M4 = m4 = x1 x2 x3,
F4 = x1 x2 x3 = M4 = m4 = x1 x2 x3,






 F5 = x1 x2 x3 = M5 = m5 = x1 x2 x3,
F5 = x1 x2 x3 = M5 = m5 = x1 x2 x3,






 F6 = x1 x2 x3 = M6 = m6 = x1 x2 x3,
F6 = x1 x2 x3 = M6 = m6 = x1 x2 x3,






 F7 = x1 x2 x3 = M7 = m7 = x1 x2 x3.
F7 = x1 x2 x3 = M7 = m7 = x1 x2 x3.
При використанні базових елементів АБО–НІ/АБО логічна схема приймає вигляд, показаний на мал.10.4.
  F F  
х1
  
 F5 F5
F
 6 6
F
F
Мал.10.4. Дешифратор “з 3 у 8”. |
Якщо на виходах реалізується неповний набір мінтермів (макстермів), то дешифратор називається неповним. Для неповних дешифраторів існують байдужі набори вхідних змінних, і їх можна використати при мінімізації вихідних функцій. У вигляді СІС у складі сучасних серій мікросхем ТТЛ випускається, наприклад, неповний дешифратор “з 4 у 10”, що використовується у пристроях виводу інформації, щоб забезпечити десяткову індикацію чи друкування двійково-десяткових чисел.
Крім пристроїв індикації дешифратори широко використовуються у пристроях керування, де вони у відповідності з надійшовшим кодом (адресою) формують керуючий сигнал, вмикаючий (чи вимикаючий) один з блоків, підключених до його виходів.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 720; Нарушение авторских прав?; Мы поможем в написании вашей работы!

 b1
b1


 a1
a1

 b
b

 2
2 a2
a2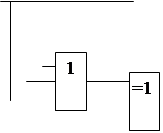
 b
b 3
3 a3
a3


 F0
F0















 х1 F2
х1 F2



 х2 F3
х2 F3

 х2
х2







 3 F4
3 F4




 5
5 F
F

 6
6

