КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Мультиплексори і демультиплексори
|
|
|
|
Мультиплексором (селектором) називається функціональний вузел, забезпечуючий передавання інформації, що може надходити по декількох вхідних інформаційних лініях х0, х1, …, хM-1, на одну вихідну лінію F. Вибір тієї чи іншої вхідної лінії здійснюється згідно з адресовим кодом S0, S1, …, Sn-1, що подається на адресовий вхід вузла. При наявності n адресових входів реалізується M = 2n комбінацій адресових сигналів, і кожна комбінація відповідає вибору однієї з М вхідних ліній. Найчастіше використовуються мультиплексори “з 4 у 1” (М = 4, n =2), “з 8 у 1” (М = 8, n = 3), “з 16 у 1” (М = 16, n = 4).
| S0 | S1 | F |
| x0 | ||
| x1 | ||
| x2 | ||
| x3 |
| Таблиця 10.2 |
 Використовуючи табл.10.2, що описує функціонування мультиплексора “з 4 у 1”, отримуємо вираз для його вихідної функції:
Використовуючи табл.10.2, що описує функціонування мультиплексора “з 4 у 1”, отримуємо вираз для його вихідної функції:





 F = х0 S0S1 х1S0S1 х2S0S1 х3S0S1.
F = х0 S0S1 х1S0S1 х2S0S1 х3S0S1.
 x2 x2
Мал.10.5. Логічна схема мультиплексора |
Відповідна логічна схема показана на мал.10.5.
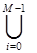 У загальному випадку вихідна функція мультиплексора “ з М у 1” приймає вигляд
У загальному випадку вихідна функція мультиплексора “ з М у 1” приймає вигляд
F = хimi,
де mi – мінтерм адресових змінних S0, S1, …, Sn-1; n = log2M.

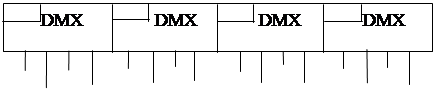
Мультиплексування при великій кількості вхідних ліній М можна виконувати пірамідальним каскадуванням мультиплексорів. На мал.10.6 наведено приклад мультиплексування “з 16 у 1” за допомогою каскадування мультиплексорів “з 4 у 1”.
У сучасних цифрових системах мультиплексори часто використовуються для отримання різних логічних функцій. Оскільки вихідна функція мультиплексора містить усі мінтерми n змінних, при подаванні на інформаційні входи відповідних значень функції, можна отримати будь-яку подану функцію n змінних. Для реалізації за допомогою мультиплексорів з n адресовими входами логічної функції m (m > n) змінних, застосовують її декомпозицію.
     x1 x3 x5 x7 x9 x11 x13 x15 x1 x3 x5 x7 x9 x11 x13 x15
          x0 x2 x4 x6 x8 x10 x12 x1 x0 x2 x4 x6 x8 x10 x12 x1 4 4
   S0 S0
F Мал.10.6. Каскадування мультиплексерів “з 4 у 1”. |
 S0  S0 S0
 
 S1 S1
Мал.10.7. Демультиплексор “з 1 у 4”. |
Для поновлення мультиплексованої інформації використовуються демультиплексори, які згідно з прийнятою адресою спрямовують інформацію у одну з М вихідних ліній. При цьому на інших виходах підтримується логічний 0. Вихідні функції демультиплексора “з 1 у М” мають вигляд Fi = xmi, де х – значення входу.
 Розглянемо приклад реалізації демультиплексора “з 1 у 4” на елементах АБО-НІ. Вихідні функції мають вигляд:
Розглянемо приклад реалізації демультиплексора “з 1 у 4” на елементах АБО-НІ. Вихідні функції мають вигляд:






 F0 = xS0S1 = x S0 S1,
F0 = xS0S1 = x S0 S1,







 F1 = xS0S1 = x S0 S1,
F1 = xS0S1 = x S0 S1,







 F2 = xS0S1 = x S0 S1,
F2 = xS0S1 = x S0 S1,



 F3 = xS0S1 = x S0 S1.
F3 = xS0S1 = x S0 S1.
Логічна схема, виконуюча ці функції, показана на мал.10.7. При великому значенні М демультиплексування здійснюється за допомогою каскадного з’єднання демультиплексорів з меншим значенням М. Приклад демультиплексора “з 1 у 16”, побудованого на демультиплексорах “з 1 у 4”, наведений на мал.10.8.
x
   S3
S S3
S  2 2
F0 F2 F4 F6 F8 F10 F12 F14 F1 F3 F5 F7 F9 F11 F13 F15
Мал.10.8. Каскадування демультиплексерів “з 1 у 4”. |
При х = 1 демультиплексор виконує функції повного дешифратора, а при х = 0 на усіх виходах встановлюється логічний 0. Таким чином демультиплексор можна використовувати, як дешифратор, що керується сигналом на вході х.
Шляхом послідовного вмикання мультиплексорів і демультиплексорів, з’єднують групу джерел інформації з групою приймачів. Вибір адресових кодів визначає від якого джерела до якого приймача передається інформація. При одночасному (паралельному) передаванні багаторозрядного числа використовують паралельне вмикання розглянутих вище однорозрядних мультиплексорів і демультиплексорів.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1251; Нарушение авторских прав?; Мы поможем в написании вашей работы!

 S0 S0
S0 S0



 S1 S1
S1 S1



 x3
x3







 F F
F F

 x1
x1





 S1
S1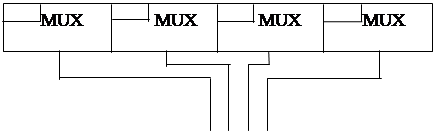

 S2
S2
 S3
S3










 F3
F3
 х1
х1







 S1 F2
S1 F2







 F1
F1








 x F0
x F0