Перший алгоритм Гоморі

Перед тим, як розглянути правильне відтинання у цьому алгоритмі, зупинемося на таких означеннях.

Цілою частиною дійсного числа a називається максимальне ціле число, що позначається як [a] і задовольняє умові [a] £ a.

Дробовою частиною дійсного числа a називається дійсне число, що позначається як {a} і задовольняє умові {a} = a - [a].

З цих означень безпосередньо прямує, що дробова частина числа завжди є невід’ємним числом. Наприклад, [-2,3] = -3, а {-2,3} = 0,7.

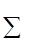Тепер перейдемо до побудови правильного відтинання. Нехай на поточній ітерації при застосуванні симплекс-методу отримано нецілочисельний розв’язок x^*, у якого координата, що відповідає i-му рядку симплекс-таблиці дробова. Рівняння, відповідаюче цьому рядку, має вигляд

x_k + a’_ij x_j = b’_i, (12.8)

j N

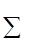де N – множина індексів небазисних змінних, x_k - базисна змінна і {b’_i} > 0. За рівнянням (12.8) побудуємо нерівність

-{b’_i} + a’_ij x_j 0. (12.9)

j N

Теорема 12.2 (Про правильне відтинання) Обмеження (12.9) є правильним відтинанням.

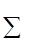Доведення. Для доведення теореми досить показати, що для обмеження (12.9) виконуються обидві умови правильного відтинання. Розв’язок x^* обмеженню (12.9) не задовольняє, оскільки {b’_i} > 0, і

a’_ij x^*_j = 0,

j N

бо у розв’язку x^* усі небазисні змінні дорівнюють нулю. Отже умова 1) виконується.

Дата добавления: 2014-01-13