Множення й ділення додатних раціональних чисел

Нехай відрізок а — сумірний з одиничним відрізком е₁ а відрізок е₁ — з відрізком е₂, причому а = 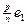, е₁ = е₂, тобто па =• ре₁,

kе₁ = qе₂. Тоді (пk) а = (рk) е₁, (рk) е₁ = (рq)е₂. Звідси (nk) а = (pq)е₂. Остання рівність показує, що довжина відрізка а при одиничному

відрізку е₂ виражається дробом 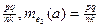. Проте за умо­вою 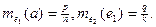Тому щоб виконувалася властивість мультиплікативності

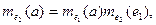
треба, щоб

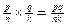
Наведені міркування приводять до такого природного означення. Означення 17. Нехай а, b Є Q₊ і нехай ці числа зображуються дробами 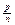і . Добутком аb називається додатне раціональне число, що зображується дробом 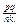. Числа а і b називають множниками, а опе­рацію знаходження добутку — множенням.

Теорема 26. Для будь-яких додатних раціональних чисел а і b існує добуток аb і при тому єдиний.

Доведення. Справедливість першої частини теореми випливає з означення добутку. Доведемо другу частину теореми. Покажемо,

що добуток аb не залежить від вибору дробів 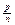і , Що зображують числа а і b, тобто

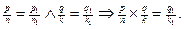
Справді, якщо 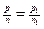i 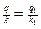, то pn₁=np₁ i qk₁=kq₁.

Перемноживши ці рівності, дістанемо

(рп₁) (qk₁) = (np₁)(kq₁), або (pq)(n₁k₁) = (nk)(p₁q₁).

Звідси

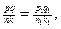
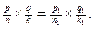
Теорему доведено.

Зазначимо, що коли натуральні числа розглядати як елементи множини Q₊, то множення їх за наведеним означенням зводиться дп івнчайного множення натуральних чисел. Справді, нехай р, q Є N.

Розглядаючи ці числа як елементи Q₊, можна зобразити їх відповідно дробами 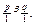Тому їхній добуток за означенням дорівнює числу, що зображується дробом

Теорема 27. Операція множення додатних раціональних ч исел мав властивості:

комутативності

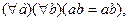a, b Є Q₊

Асоціативності

0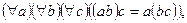a, b, c Є Q₊

дистрибутивності відносно додавання

(а) (b) (с) ((а + b)с = ас + bс), а, b, сЄ Q+;

монотонності

(а) (b) (с)(а<b ас<bс), а, b, с Є Q+.

Доведення всіх сформульованих властивостей безпосередньо ви¬пливає з відповідних властивостей множення у множині N. якщо врахувати означення 13, 14, 17.

Вище означили добуток двох додатних раціональних чисел. Добу­ток п додатних раціональних чисел (п > 2) означають так само, як у випадку цілих чисел (див. п. 16.7).

Ділення додатних раціональних чисел вводиться як операція, обернена до операції множення.

Означення 18. Часткою додатних раціональних чисел а і b назива­ють таке додатне раціональне число с = а: b, що сb = а. Число a називають діленим, b — дільником, а операцію знаходження част­ки — діленням.

Теорема 28. Для будь-яких додатних раціональних чисел а і b існує частка а: b і при тому єдина.

Доведення. Нехай а, b Є Q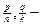₊, дроби, що зображують відповідно ці числа. Позначимо через с додатне раціональне число, що зображується дробом 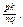Тоді 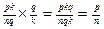, тобто cb = a. Отже, c= a: b, тобто частка існує.

Доведемо єдиність частки. Припустимо, що існують дві частки: с₁ = a: b, c₂ = a: b. Тоді за означенням маємо:

c₁b = a, c₂b = c, тому c₁b = c₂b. Якби с₁ ≠ с₂, то згідно з властивістю монотонності множення, c₁b ≠ c₂b. Отже, с₁ = с₂.

Теорему доведено.

Зазначимо, що будь-який дріб можна розглядати як частку від ділення його чисельника на знаменник. Справді, нехай р, q Є N. Тоді

p: q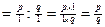

Якщо дано дріб 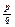, то

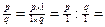p i q.

Дата добавления: 2014-01-13