Числові вирази

ВИРАЗИ

Тема. РІВНЯННЯ, НЕРІВНОСТІ, ФУНКЦІЇ

ОЗНАЧЕННЯ ПОНЯТЬ ШКІЛЬНОГО КУРСУ МАТЕМАТИКИ

ЗАСТОСУВАННЯ ТЕОРІЇ МНОЖИН І МАТЕМАТИЧНОЇ ЛОГІКИ ДО

Семестр

Математика

Поняття виразу, числових рівностей і нерівностей, рівняння і нерівності зі змінними, їх системи і сукупності широко застосовуються в різних науках, тому їх вивченню приділяється велика увага. Всі ці поняття можуть бути по-різному означені. Серед них найбільш простими і науково точними є ті, що базуються на використанні теорії множин і математичної логіки.

Під числовим виразом розуміють запис чисел та операцій над ними, в якому за попередньою домовленістю відомий порядок виконання операцій над ними. Кожне число є також числовим виразом. Числа виразу називаються його компонентами.

Порядок операцій у числовому виразі регулюється круглими дужками: спочатку операції виконуються у найглибших дужках, потім у наступних і т.д., зовнішні дужки опускаються. Якщо ж дужки в числовому виразі відсутні, то порядок виконання арифметичних операцій такий: множення або ділення, потім додавання або віднімання в порядку їх запису.

Говорячи про числові вирази, мають на увазі, що результати зазначених у них операцій існують, тобто операції виконувані. Але якщо в числовому виразі є, наприклад, операція ділення з дільником, рівним нулю, то її результат не існує. В цьому разі кажуть, що числовий вираз не має смислу. Зокрема, числовий вираз (4 + 5): (6 – 2 × 3) не має смислу, бо при виконанні зазначених операцій у ньому з’являється необхідність ділення на нуль.

Якщо в числовому виразі виконати всі зазначені операції, то одержане число називається його значенням. Якщо числовий вираз є числом, то це число і називається його значенням. Залежно від значень числові вирази поділяються на додатні, від’ємні і нульові, записується це так: А > 0, А < 0, А = 0. Числові вирази не завжди мають значення в тій числовій множині, з якої беруть їх компоненти. Наприклад, числовий вираз 15: (4 – 7) не має значення у множині натуральних чисел, бо різниця чисел 4 і 7 не має значення у множині натуральних чисел. Хоча компоненти і значення виразів (3 – 8) + (14 – 3) і ((1 + + 8): 18) × 6 є натуральними числами, але їх не можна розглядати над множиною натуральних чисел, бо результати проміжних операцій 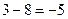і 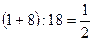не є натуральними числами. Це пояснюється тим, що не всі операції є виконуваними над певними числовими множинами. При розгляді числових виразів в усіх випадках, коли не вказано, з яких числових множин беруться їх компоненти, мають на увазі множину дійсних чисел.

Числовим виразам при потребі дають назви за останніми в них операціями. Наприклад, вираз 4 + 36: 9 називають сумою числа 4 і частки чисел 36 і 9.

Числові вирази не є висловленнями, бо про них не можна сказати, істинні вони чи хибні. Домовимося позначати числові вирази великими латинськими буквами, а множину всіх виразів – W.

З числовими виразами знайомляться вже учні початкових класів. Спочатку з виразами виду 5 + 3, 8 – 2, називаючи їх відповідно сумою і різницею. Потім розглядаються числові вирази дедалі складнішої структури. Терміни "математичний вираз", "значення виразу" з’являються в лексиконі учнів, коли вони вже виконують обчислення в межах сотні. В процесі навчання учні знаходять значення числових виразів; записують розв’язок, коли це можливо і є потреба, текстової задачі у вигляді числового виразу; складають за даними виразами задачі. При виконанні таких завдань вони неминуче зустрічаються з числовими виразами, значення яких не можна знайти у множині натуральних чисел. Наприклад, про вираз 4-7 учні говорять, що його значення не можна знайти, бо не можна від меншого числа відняти більше.

Дата добавления: 2014-01-13