Числові рівності та їх властивості

Два числових вирази називаються рівними, якщо рівні їх числові значення. Відношення рівності на множині числових виразів є відношенням еквівалентності, бо таким воно є для числових множин, а тому визначає розбиття на класи рівних між собою виразів. Це дає змогу в усіх випадках, коли цікавляться значенням виразу, а не його структурою, заміняти один вираз на рівний йому. Наприклад, вираз 4 + 4 + 4 + 4 + 4 можна замінити виразом 4 × 5 або 20.

Два довільних числові вирази А і В, з’єднані між собою знаком рівності „=”, утворюють числову рівність (записується А = В). Числові вирази А і В називаються частинами числової рівності: А – лівою, В – правою.

З точки зору математичної логіки числова рівність є висловленням, яке істинне тоді і тільки тоді, коли значення лівої частини дорівнює значенню правої частини. Істинне висловлення, що визначається числовою рівністю, часто називають істинною (правильною) числовою рівністю. Над числовими рівностями як над висловленнями можна виконувати всі операції логіки висловлень, зокрема кон’юнкцію і диз’юнкцію.

Істинні числові рівності мають властивості, що базуються на властивостях дійсних чисел.

1. Якщо до обох частин числової рівності додати (відняти) один і той же числовий вираз, то знову одержимо числову рівність:

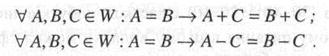
Відношення рівності числових виразів має рефлексивну властивість, тому для довільних числових виразів А і С

А + С = А + С (1)

За умовою А = В. Замінивши А на В у правій частині рівності (1), на підставі симетричної властивості відношення рівності одержуємо

А + С = В + С.

Наслідок 1. Якщо одна з частин числової рівності є алгебраїчною сумою, то будь-який її доданок можна з однієї частини перенести в другу частину, але при цьому його знак змінити на протилежний, зокрема

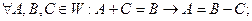
Наслідок 2. Якщо в обох частинах числової рівності є рівні доданки, то їх можна опустити, і знову одержимо числову рівність, зокрема

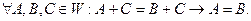
2. Числові рівності можна почленно додавати (віднімати), ізнову одержимо числову рівність, зокрема

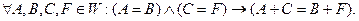
Нехай А, В, С, і F – довільні числові вирази, при яких

за властивістю 1;

за транзитивністю відношення рівності

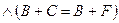для числових виразів;

.

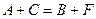Аналогічно доводяться такі властивості числових рівностей.

3. Якщо обидві частини числової рівності помножити на один і той же числовий вираз, то знову одержимо числову рівність:

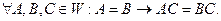
4. Якщо обидві частини числової рівності поділити на один і той же числовий вираз, значення якого відмінне від нуля, то знову одержимо числову рівність:

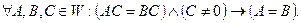
5. Числові рівності можна почленно перемножати, і знову одержимо числову рівність, зокрема

6. Обидві частини числової рівності можна почленно підносити до степеня з натуральним показником, і знову одержимо числову рівність:

7. Якщо числові вирази, відмінні від нуля, рівні між собою, то рівними будуть і обернені їм вирази:

Дата добавления: 2014-01-13