Розв’язування задач алгебраїчним методом

Навчаючи математики, велика увагу слід приділяти задачам, не кожна з яких може бути розв’язана арифметично або, якщо і розв’язується, то досить складно. Застосування ж рівнянь часто значно полегшує знаходження розв’язків задач. Метод розв’язування задач, що ґрунтується на використанні рівнянь, називається алгебраїчним.

При розв’язуванні задач алгебраїчним методом найчастіше змінними позначають числа, які потрібно знайти.

Задача 8. Розв’язати задачі алгебраїчним методом.

Відстань 36 км один із двох лижників пройшов на півгодини швидше, ніж другий. Швидкість першого лижника на 1 км/год більша, ніж другого. Визначити швидкість кожного лижника.

Швидкість другого лижника позначимо – х км/год, тоді (х + 1) км/год – швидкість першого лижника. Відстань 36 км перший лижник проходить за 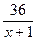годин, а другий – за годин. Різниця в часі руху другого і першого лижників дорівнює , а за умовою задачі вона становить півгодини. Отже, маємо рівняння

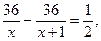
в якому, згідно з умовою задачі, х > 0.

Для знаходження розв’язків рівняння виконаємо над ним перетворення

72х + 72 – 72х = х² + х Û х² +х – 72 = 0.

Одержали квадратне рівняння, коренями якого є дійсні числа – 9 і 8. Оскільки х > 0, то корінь рівняння – 9 не буде розв’язком задачі. Таким чином, швидкість другого лижника – 8 км/год, а першого – 8 +1=9 км/год.

Відповідь: 9 км/год, 8 км/год.

2. Басейн наповнюється двома трубами за 6 год. Перша труба може наповнити весь басейн на 5 год швидше, ніж друга. За який час може наповнити басейн кожна труба окремо?

^ Об’єм басейну приймемо за 1 частину. Час, за який басейн наповнить перша труба, позначимо через х год, тоді (х + 5) год – час, за який басейн наповнить друга труба. За 1 год перша труба заповнить 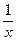частину басейну, а друга труба – 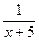частину басейну. Разом за одну годину дві труби заповнять 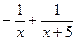– частину басейну, що дорівнює його частині, бо з умови задачі відомо, що басейн наповнюється обома трубами за 6 год. Значить, можна скласти рівняння

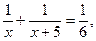
в якому, згідно з умовою задачі, х > 0.

Здійснивши перетворення над рівнянням, дістанемо

6х + 30 + 6х = х² + 5х Û х² – 7х – 30 = 0.

Квадратне рівняння, яке отримали, своїми коренями має дійсні числа – 3 і 10. Зважаючи, що х > 0, число – 3 не може бути розв’язком задачі. Отже, час, за який басейн наповнить перши труба, дорівнює 10 год, а друга труба – 10 + 5=15 год.

Відповідь: 10 год, 15 год.

Дата добавления: 2014-01-13