Рівняння з двома змінними

Поняття рівняння з однією змінною можна узагальнити на випадок рівняння з кількома змінними. Всі твердження для рівнянь з однією змінною матимуть місце і для рівнянь з кількома змінними, лише відповідно сформульовані. Розглянемо це на прикладі рівнянь з двома змінними.

Нехай на множині М =М^х х М задано два вирази f (x,y) і q (x,y) з двома змінними. Предикат

f (x,у) = q (x, у), (х,у) Î М,

для якого потрібно знайти область істинності, називається рівнянням з двома змінними.

Областю визначення рівняння з двома змінними називається область визначення предиката, що задає рівняння. Вона дорівнює перерізу областей визначення виразів f (x,y) і q (x,y).

Множиною розв’язків рівняння з двома змінними називається область істинності предиката, що задає рівняння, а кожна впорядкована пара з цієї множини – його розв’язком. Розв’язати рівняння з двома змінними – це означає знайти множину його розв’язків.

Якщо в рівнянні з двома змінними всі коефіцієнти членів, що містять змінні, і вільний член дорівнюють нулю, то довільна пара дійсних чисел буде його розв’язком. Якщо ж всі коефіцієнти членів, що містять змінні, рівні нулю, а вільний член відмінний від нуля, то таке рівняння не має розв’язків. Тому розглядаються рівняння, в яких хоч один із коефіцієнтів членів, що містять змінні, відмінний від нуля. Для одержання розв’язків такого рівняння одній із змінних, наприклад, у, надають довільне значення у₀ з множини M_y, отримують рівняння з однією змінною х. Розв’язують його. Кожне знайдене значення х₀, якщо воно існує, змінної х разом зі значенням у₀ становлять розв’язок даного рівняння з двома змінними. Оскільки значення однієї зі змінних вибиралось довільно, то в більшості випадків рівняння з двома змінними має безліч розв’язків, причому одна з його компонент вибирається довільно. Наприклад, рівняння

х² – у =0

має безліч розв’язків виду (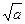, а) або (–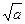, а), де а > 0; рівняння

х²+у² =0

має єдиний розв’язок (0; 0); а рівняння

х² + y²=–1

не має розв’язків.

Кожному розв’язку рівняння з двома змінними на координатній площині відповідає одна і тільки одна точка, координати якої збігаються з розв’язком. Множина всіх таких точок називається точковим графіком (коротше графіком) рівняння з двома змінними. В більшості випадків графіком рівняння з двома змінними є лінія на координатній площині.

Поняття лінії є неозначуваним у нашому курсі. Уявлення про неї можна одержати, розглядаючи, наприклад, довільно зігнутий шматок дроту. В математиці лінію розглядають як множину точок площини (простору), що мають певну, спільну для всіх цих точок, властивість. Знайомство з окремими видами ліній, таких, наприклад, як пряма, коло, парабола, еліпс тощо, передбачено шкільним курсом математики.

Рівняння з двома змінними називається рівнянням лінії на координатній площині, якщо:

1)кожний розв’язок рівняння є координатою точки лінії;

2)координати кожної точки лінії є розв’язком рівняння.

Рівняння лінії може бути складним, і задати його буває важко, але воно дає змогу встановлювати по його розв’язках властивості лінії, тобто вивчення геометричних властивостей лінії здійснювати алгебраїчними методами.

Практично розв’язуються дві задачі: спочатку за деякою однією геометричною властивістю лінії знаходять її рівняння, а потім за допомогою цього рівняння вивчають інші властивості даної лінії. Будувати лінію іноді зручніше на основі її геометричних властивостей, а іноді – за допомогою рівняння.

Розглянемо на прикладі кола, як виводиться рівняння лінії.

Колом із заданими центром у точці С і радіусом r називається множина точок площини, відстань яких від точки С площини дорівнює числу r (позначається K[С; r]).

На площині задамо довільну прямокутну систему координат О х у. Коло К[С; r]) може бути розміщене довільно відносно системи координат. Нехай точка С(а,b) – його центр і М(х, у) – довільна точка кола у вибраній системі координат, рис. 1.

Тоді СМ = r. За формулою відстані між двома точками на координатній площині знайдемо

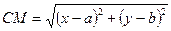
або

(1)

Оскільки r > 0 і , то рівняння (1) буде рівносильне рівнянню

(x – a)²+(y – b)²=r². (2)

Отже, якщо точка М(х, у) лежить на колі К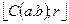, то її координати є розв’язком рівняння (2).

Навпаки, нехай (х₀у₀) – будь-який розв’язок рівняння (2), тобто

(x₀ – a)²+(y₀ – b)²=r².

Звідси одержуємо, що

а це означає, що відстань від точки М (х₀, у₀) до точки С(а, b) дорівнює r. Тому точка М (х₀, у₀) лежить на колі К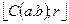. Таким чином, має місце теорема.

Теорема 5. У прямокутній системі координат хОу рівняння кола радіусом r і з центром в точці С(а, b) може бути записане у вигляді

(x – a)²+(y – b)²=r². (2)

Зокрема, коло з центром у початку координат має рівняння

х²+у²=r².

Рівняння (2) називається зведеним (канонічним) рівнянням кола. Якщо в ньому розкрити дужки, то одержимо рівняння другого степеня з двома змінними, яке називається загальним рівнянням кола.

Але не кожне рівняння другого степеня з двома змінними є рівнянням кола на площині. Так, рівняння у = х² визначає лінію, яка називається квадратною параболою.

Задача 9. Довести, що рівняння

х² +у² + 4х – 8у + 11 =0

є рівнянням кола. Знайти його центр і радіус.

Щоб довести, що дане рівняння є рівнянням кола, потрібно звести його до канонічного вигляду. Для цього в лівій частині рівняння виділимо повні квадрати

х² + у² + 4х – 8y +11 =

= (х² + 2×2х + 4) + (y² – 2×4y + 16) – 4 – 16 + 11 =

= (x + 2)² + (y – 4)² – 9.

Отже,

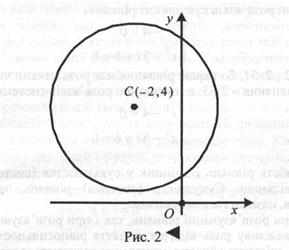
(х + 2)² + (y – 4)² – 9 = 0 або (х + 2)² + (y – 4)²=3².

А це і є канонічним рівнянням кола з радіусом 3 і центром (–2; 4), рис. 2.

До найпростіших ліній на площині належить пряма, яка задається рівнянням першого степеня з двома змінними:

ax + by = c, a, b, c, x, y Î R,

де а і b одночасно не дорівнюють нулю, тобто а² + b² ¹ 0.

Дата добавления: 2014-01-13