Сукупності і системи рівнянь

Сукупністю рівнян ь називається диз’юнкція рівнянь (позначається квадратною дужкою зліва).

Системою рівнянь називається кон’юнкція рівнянь (позначається фігурною дужкою зліва).

Поняття, що стосуються сукупностей і систем рівнянь, встановлюються на основі властивостей диз’юнкції і кон’юнкції предикатів. Область визначення сукупності (системи) рівнянь дорівнює перерізу областей визначення рівнянь сукупності (системи) Множина розв’язків сукупності (системи) рівнянь дорівнює об’єднанню (перерізу) множин розв’язків кожного з рівнянь сукупності (системи). Для знаходження множини розв’язків сукупності (системи) рівнянь потрібно розв’язати кожне з її рівнянь, а потім знайти об’єднання (переріз) одержаних множин. Воно і буде множиною розв’язків сукупності (системи) рівнянь. Наприклад, множиною розв’язків сукупності рівнянь

буде { – 2; 2; 3}, бо перше рівняння має розв’язками числа – 2 і 2, а друге рівняння – 2 і 3; а множиною розв’язків системи рівнянь

буде { 2 }.

Кількість рівнянь і змінних у сукупностях (системах) може бути довільною. Сукупність (система) рівнянь, що не має розв’язків, називається несумісною.

Як при розв’язуванні рівнянь, так і при розв’язуванні систем рівнянь, важливу роль відіграє поняття рівносильності. Системи рівнянь зі спільною областю визначення називаються рівносильними на ній, якщо множини їх розв’язків збігаються. Якщо системи не мають розв’язків, то вони також вважаються рівносильними. Рівносильність значність систем рівнянь залежить від їх області визначення: зміна її може привести до порушення рівносильності. Наприклад, системи рівнянь

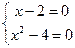i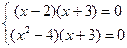

рівнозначні на множині натуральних чисел і нерівнозначні на множині цілих чисел, бо на множині натуральних чисел їх множинами розв’язків є множина {2}, а на множині цілих чисел множиною розв’язків першої системи є множина {2}, а другої – {2, – 3}.

Скориставшись теоремами про рівносильність рівнянь можна довести теорему.

Теорема 6. Якщо в системі рівнянь хоч одне рівняння замінити йому рівносильним, то одержимо систему рівнянь, рівносильну даній на її області визначення.

Існують алгебраїчні і геометричні способи розв’язування систем рівнянь. Розглянемо їх на прикладі систем рівнянь з двома змінними. Алгебраїчні способи полягають у тому, що систему рівнянь за допомогою перетворень замінюють рівносильною їй системою, в якій одне з рівнянь містить лише одну змінну або всі коефіцієнти членів, що містять змінні, дорівнюють нулю. Розв’язки такої системи, якщо вони існують, легко знайти. Вони і будуть розв’язками даної системи рівнянь. З алгебраїчних способів найбільш вживаними є способи алгебраїчного додавання і підстановки, які відомі ще з шкільного курсу математики.

Геометричний спосіб розв’язування системи рівнянь із двома змінними полягає в тому, що на координатній площині будують лінії, які визначаються кожним із рівнянь системи. Координати точок перетину цих ліній і будуть розв’язками системи. Якщо лінії не перетинаються, то система несумісна.

Задача 10. Розв’язати алгебраїчно систему рівнянь:

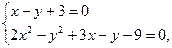
Перше рівняння системи є рівнянням першого степеня. Виразимо з нього х через у:

х = у – 3.

Підставимо вираз у – 3 замість х у друге рівняння системи. Дістанемо рівняння

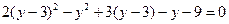
яке після розкриття дужок і зведення подібних членів запишеться

у² – 10у = 0.

Воно має два корені: у₁ = 0 і у₂ = 10.

Підставимо ці числа у вираз у – 3 замість у, одержимо х₁ = = – 3 і x₂ = 7. Отже, дана система рівнянь має два розв’язки:

х¹ = –3, у₁ = 0 і х₂ = 7, у₂= 10.

Відповідь: {(– 3; 0), (7; 10)}.

Задача 11. Розв’язати графічно систему рівнянь:

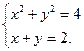
Задамо на площині довільну прямокутну систему координат Оху і побудуємо на координатній площині лінії, що визначаються рівняннями даної системи. Графіком першого рівняння х² + у² = 4 є коло з центром у початку координат і радіусом r = 2.

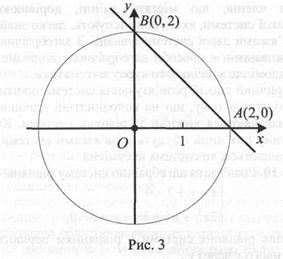
Графіком другого рівняння х + у = 2 є пряма (рис. 3).

Точки перетину ліній позначимо А(0; 2) і В(2; 0). Отже, система рівнянь має два розв’язки: (0; 2) і (2; 0).

Відповідь: {(0;2),(2;0)}.

Дата добавления: 2014-01-13