Уравнения одномассовых механических частей электроприводов

Основные понятия

Механическая часть электропривода

Механическая часть электропривода – это совокупность входящих в него таких устройств как ЭДУ, МПУ и РОМ.

С точки зрения механики механическая часть электропривода, в том числе АЗЭП, представляет собой систему масс, связанных механическими элементами и движущихся с различными скоростями вращательно и/или поступательно [3, с.24]. Механические элементы связи в процессе работы деформируются, т.к. не являются абсолютно жесткими. Механические части в зависимости от количества деформируемых механических элементов связи (или, коротко говоря,вдеформируемых связей) разделяют на одномассовые и многомассовые.

Механическая часть называется одномассовой, если можно считать, что она не содержит деформируемых связей. В противном случае механическая часть называется многомассовой.

Различают частные случаи многомассовых механических частей: двухмассовые, трехмассовые и т.д. Например, двухмассовой называют механическую часть, содержащую одну деформируемую связь, а трехмассовой – две деформируемые связи. Можно показать, что одномассовые механические части описываются системой уравнений, которые можно свести к системе, содержащей только одно дифференциальное уравнение, а двухмассовые – к системе, содержащей только два дифференциальных уравнения, и.т.д.

Будем полагать первоначально для простоты, что механическая часть содержит только ЭДУ и РОМ, т.е. МПУ отсутствует. Кинематическая схема такой механической части приведена на рис.1.1. Поясним эту схему. ЭДУ создает электромагнитный момент М, под действием которого РОМ приходят в движение.

Рис.1.1. Кинематическая схема механической части электропривода

без МПУ

В ходе движения РОМ совершают определенную работу, оказывая тем самым определенное сопротивление электродвигателю, которое можно охарактеризовать определенным моментом сопротивления 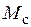. Момент сопротивления 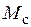в теории электропривода называют также статическим моментом [2, с.19]. Под действием моментов М и 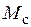ротор ЭДУ и РОМ вращаются с угловой скоростью ω.

Из курса теоретической механики известно, что движение механического объекта определяется вторым законом Ньютона. Для твердого тела, которое совершает вращение вокруг неподвижной оси, второй закон Ньютона представляется уравнением [2, с.16].

, (1.1)

где – k -й момент силы, k = 1,…, N; J – момент инерции тела; – угловая скорость вращения тела.

Рассматриваемая одномассовая механическая часть представляет собой твердое вращающееся тело. Поэтому можно использовать уравнение (1.1), которое в данном случае принимает вид

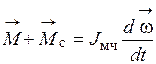, (1.2)

где 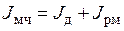– суммарный момент инерции всех элементов механической части; – момент инерции ЭДУ; J _рм– момент инерции РОМ.

Векто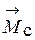ры , , направлены, очевидно, вдоль оси вращения элементов механической части. При этом векторы 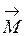и совпадают по направлению, а вектор 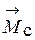направлен против вектора , т.к. эти моменты противодействуют друг другу. С учетом изложенного уравнение (1.2) можно упростить, записав его в проекциях на ось вращения рассматриваемой механической части в следующем виде:

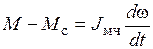. (1.3)

Уравнение (1.3) называют основным уравнением движения электропривода.

Рассмотрим далее более сложную одномассовую механическую часть электропривода. Для определенности будем полагать, что она состоит из ЭДУ, редуктора (Р) и РОМ. Кинематическая схема такой системы представлена на рис.1.2. Редуктор Р здесь исполняет роль МПУ.

M M p1

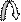
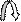
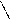
ЭДУ w2 M p2 M c

Р РОМ

Рис.1.2. Кинематическая схема механической части электропривода

с МПУ в виде редуктора Р

Для математического описания указанной системы (рис.1.2) необходимо составить в отличие от ранее рассматриваемой простейшей системы (рис1.1) не одно, а несколько уравнений. Покажем, что эти уравнения могут быть сведены к одному эквивалентному уравнению, совпадающему по форме с основным уравнением движения (1.3).

Составим вначале уравнение механического движения для каждой оси механической части. При составлении уравнения для оси двигателя будем полагать, что, во-первых, на ней действует электромагнитный момент двигателя М и противодействующий ему со стороны редуктора момент сопротивления , и, во-вторых, вращение вала двигателя происходит с угловой скоростью . Направления указанных величин показаны на рис.1.2. Итак, запишем по второму закону Ньютона для оси двигателя уравнение

, (1.4)

где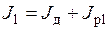– результирующий момент инерции всех элементов вращающихся на оси двигателя; 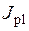– момент инерции верхнего колеса редуктора.

Для оси РОМ, учитывая, что на этой оси действуют силовой момент редуктора 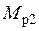, который приводит РОМ во вращение, и противодействующий ему момент сопротивления 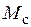РОМ (рис.1.2), уравнение движения имеет вид

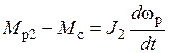, (1.5)

где – результирующий момент инерции всех элементов вращающихся на оси РОМ; – момент инерции нижнего колеса редуктора; 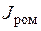– момент инерции РОМ.

Угловые скорости осей редуктора в предположении, что редуктор является абсолютно жестким элементом и не имеет зазоров, связаны уравнением

, (1.6)

где i – передаточное число редуктора.

Так как в трех записанных уравнениях (1.4)–(1.6) содержится четыре неизвестных величины (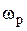, , , 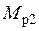), то для описания механической части необходимо привлечь закон сохранения механической мощности при преобразовании ее через редуктор. Таким образом, для записи закона сохранения необходимы формулы для механических мощностей. Из курса механики известно, что механическая мощностьна валу, создаваемая моментом , при условии, что вал вращается с угловой скоростью 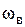, задается равенством

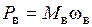. (1.7)

Учитывая равенство (1.7), можно записать, что механическая мощность , развиваемая моментом верхнего колеса редуктора, задается равенством

. (1.8)

Аналогично мощность , развиваемая нижним колесом редуктора, задается равенством

. (1.9)

При записи закона сохранения механической мощности, преобразуемой редуктором, учтем, что в рассматриваемом редукторе мощность может передаваться как от верхнего вала к нижнему, так и наоборот. Передача мощности от нижнего вала к верхнему возможна, например, в том случае, когда двигатель обесточивается, а РОМ по инерции совершает движение. Будем полагать, что редуктор преобразует механическую мощность верхнего вала в механическую мощность нижнего вала с КПД , а механическую мощность нижнего вала в механическую мощность верхнего вала – с КПД . Очевидно, что направление преобразования мощности можно определить по знаку угловой скорости вала двигателя . При >0 мощность передается от верхнего вала к нижнему, а при <0 – от нижнего к верхнему.

Учитывая изложенное, по закону сохранения механической мощности при преобразовании ее в редукторе можно записать:

, (1.10)

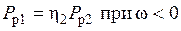. (1.11)

Из (1.11) следует, что

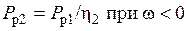. (1.12)

Тогда равенства (1.10) и (1.12) можно представить так:

, (1.13)

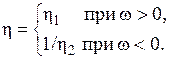(1.14)

Итак, в результате проведенных рассуждений показано, что механическая часть, кинематическая схема которой приведена на рис.1.2, может быть описана шестью уравнениями (1.4)–(1.6), (1.8), (1.9) и (1.13). Эти уравнения содержат шесть неизвестных величин: 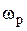, , , , , 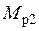. Это означает, что при заданных силовых моментах М и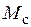механическая часть электропривода описывается однозначно. Нетрудно показать (это необходимо выполнить САМОСТОЯТЕЛЬНО), что указанные шесть уравнений сводятся к одному дифференциальному уравнению, которое имеет следующий вид:

, (1.15)

, (1.16)

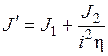, (1.17)

где – приведенный статический момент нагрузки; 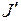– приведенный момент инерции.

Сравнивая уравнение (1.3) механической части без МПУ с уравнением (1.15) механической части с МПУ в виде редуктора, приходим к выводу о том, что по форме эти уравнения совпадают. При этом уравнение (1.15) получается из уравнения (1.3) путем замены реальных величин 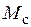и на приведенные величины и 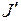. Следовательно, для составления уравнения движения механической части с МПУ в виде редуктора необходимо составить уравнение движения (1.3) механической части без МПУ, заменив в нем реальные величины приведенными величинами по формулам (1.16) и (1.17).

Замена в уравнении движения электропривода реальных величин приведенными называется приведением моментов сопротивления и моментов инерции к валу двигателя.

Можно показать, что уравнение движения механической части электропривода для любой кинематической схемы имеет вид (1.15). Однако формулы расчета приведенного статического момента нагрузки и приведенного момента инерции 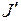зависят от кинематической схемы электропривода.

В случае МПУ в виде редуктора уравнения приведения (1.16) и (1.17) показывают, что понижающий редуктор, т.е. редуктор с передаточным числом i > 1, существенно ослабляет влияние на двигатель статического момента нагрузки и момента инерции нагрузки.

Дата добавления: 2014-01-13