Где – индуктивность статорных обмоток. Таким образом, индуктивное сопротивление также будет изменяться в 100…10000 раз. При принятых допущениях ток холостого хода

Следовательно, необходимо в силу (3) и (4), чтобы частота также изменялась бы в 100…10000 раз. Индуктивное сопротивление статорных обмоток

, (5)

, (6)

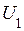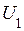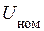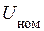где – действующее фазное статорное напряжение. Если =, где – номинальное фазное статорное напряжение, то при 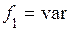ток 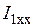будет изменяться в таком же широком диапазоне, как и частота , и может существенно превысить номинальное значение тока статорных обмоток.

Из изложенного следует, что при изменении (регулировании) частоты статорных напряжений необходимо изменять также и их действующее значение 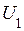. Установим необходимый закон взаимосвязи величин и 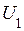, рассматривая работу АД на холостом ходу. Пренебрегая активным сопротивлением, можно записать для произвольных и номинальных значений величин 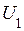и

, (7)

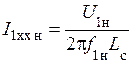, (8)

где , , 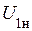– номинальные значения величин соответственно , , .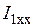

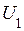Разделим соотношение (7) на соотношение (8), в результате чего получим

. (9)

Откуда

. (10)

Из (10) видно, что если 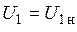, то ток 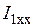при уменьшении частоты 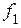будет пропорционально возрастать. Потребовав выполнения условия

, (11)

получим в силу (10) и (11) закон взаимосвязи величин и 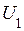, при частотном управлении АД в следующем виде:

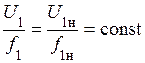. (12)

Закон (12) называется пропорциональным законом или законом Костенко.

Применяются также и другие подходы для определения связи величин 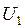и 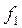. Основной подход основывается на поддержании постоянства перегрузочной способности АД (), т.е. на обеспечении условия

. (13)

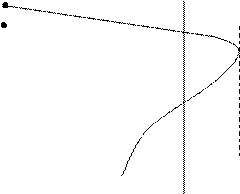
Поясним необходимость обеспечения условия (13) графически (см. рисунок 2).

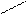
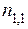
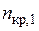
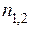
0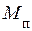

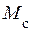
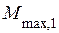
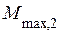
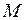
Рисунок 2 – Семейство МХ АД

Если уменьшать частоту 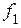, то увеличивается согласно формуле

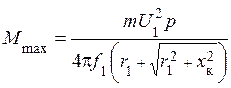, (14)

где 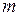– количество фаз АД; 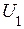– статорное фазное напряжение; 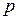– количество пар полюсов; 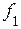– частота статорных напряжений; 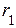– активное сопротивление одной фазы обмотки статора; 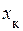– индуктивное сопротивление короткого замыкания.

Сопротивление 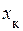задается соотношением

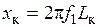, (15)

где – индуктивность короткого замыкания.

Пусть момент сопротивления 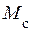на валу не изменяется. Таким образом, из рисунка 2 видно, что при большой частоте 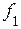запас по моменту (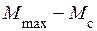) незначителен, а при небольшой частоте 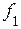указанный запас достаточно велик. Однако запас по моменту всегда должен оставаться достаточно большим, чтобы случайные нагрузки не привели к остановке двигателя. Полагают, что АД будет обладать требуемым запасом по моменту, если обеспечить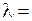 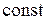. Обычно 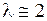. Рассмотрим в этом случае связь величин 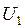и 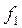. Для простоты положим, что определяется по упрощенной формуле при условии, что 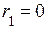. Тогда

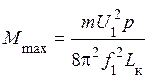. (16)

Подставив (16) в (13), найдем связь между 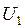и 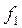в виде

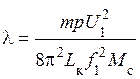. (17)

Из (17) следует, что

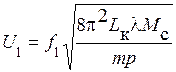. (18)

Введем обозначение

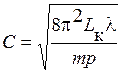, (19)

где 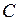– константа.

Тогда соотношение (18) можно записать так:

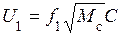. (20)

Соотношение (20) задает взаимосвязь общего вида между величинам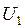и и 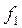, которая учитывает, что момент 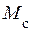изменяется на валу при изменении частоты вращения АД.

Рассмотрим варианты изменения момента сопротивления .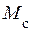

1. Если во всех рабочих режимах , то тогда

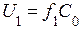, (21)

где 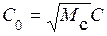– константа.

Выражение (21) представляет собой пропорциональный закон.

2. Пусть 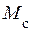– вентиляторный момент сопротивления, т.е.

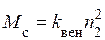, (22)

где 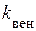– коэффициент.

Учитывая, что 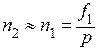, то тогда выражение (22) можно преобразовать к виду

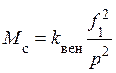. (23)

Таким образом, получим

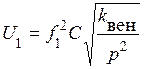. (24)

Выражение (24) представляет собой квадратичный закон.

Существуют и другие законы, которыми связаны величины 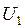и .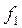

Приходим, таким образом, к выводу, что для реализации частотного управления требуется преобразователь частоты и напряжения (ПЧН). Функциональная схема ПЧН представлена на рисунке 3.

Дата добавления: 2014-01-13