
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
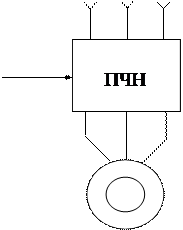
Преобразователи частоты и напряжения
|
|
|
|
Сеть
 |
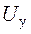
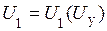 ;
; 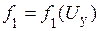
Рисунок 3 – Функциональная схема ПЧН, предназначенного для реализации частотного управления АД
Функции 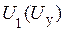 и
и 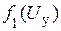 должны быть таковы, чтобы реализовать соотношение (20). Для определения функций
должны быть таковы, чтобы реализовать соотношение (20). Для определения функций 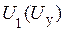 и
и 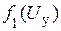 преобразуем соотношение (20) к виду
преобразуем соотношение (20) к виду
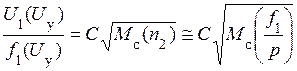 . (25)
. (25)
Решив (25), можно установить необходимый вид функций 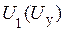 и
и 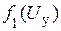 .
.
Классификацияпреобразователей частоты и напряжения(ПЧН) представлена на рисунке 4.
 |
Рисунок 4 – Классификация ПЧН:
ОК – оконечный каскад; АИН – автономный инвертор напряжений; АИТ – автономный инвертор тока.
Автономный инвертор напряжения (АИН) – это преобразователь постоянного напряжения в переменное, обладающий свойствами источника напряжения. В регулируемом АИН регулируется действующее значение его выходного напряжения.
Автономный инвертор тока (АИТ) – это преобразователь постоянного напряжения в переменное, обладающий свойствами источника тока. В регулируемом АИТ регулируется действующее значение его выходного тока.
Статические ПЧН на основе УВ и АИН. Рассмотрение указанных ПЧН начнем с их оконечного каскада – АИН. В общем случае различают однофазные и трехфазные АИН.
Рассмотрим принцип действия трехфазного АИН. Упрощенная функциональная схема такого АИН, подключенного к трехфазному асинхронному двигателю, приведена на рис. 1, где К1, …, К6 – ключи.
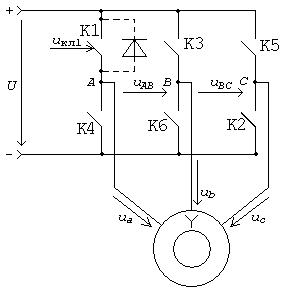
Рис.1. Упрощенная функциональная схема трехфазного АИН
Трехфазный АИН имеет 2 шины постоянного напряжения 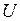 , между которыми включены 3 параллельных плеча АИН, каждое из которых содержит по 2 ключа. Ключи могут быть тиристорными или транзисторными. В настоящее время, как правило, используются транзисторные ключи. Каждый ключ содержит дополнительные элементы: защитный диод и снаббер. Последний обеспечивает изменение тока ключа по заданному закону. Из всех шести защитных диодов на рис. 1 для простоты показан только один диод, который включен параллельно ключу К1. Снабберы ключей на рис. 1 не показаны.
, между которыми включены 3 параллельных плеча АИН, каждое из которых содержит по 2 ключа. Ключи могут быть тиристорными или транзисторными. В настоящее время, как правило, используются транзисторные ключи. Каждый ключ содержит дополнительные элементы: защитный диод и снаббер. Последний обеспечивает изменение тока ключа по заданному закону. Из всех шести защитных диодов на рис. 1 для простоты показан только один диод, который включен параллельно ключу К1. Снабберы ключей на рис. 1 не показаны.
На каждый ключ подается свое управляющее напряжение. Например, на ключ К1 подается управляющее напряжение 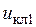 . Следовательно, ключи могут работать автономно. Рассмотрим простейший способ подачи управляющих напряжений и соответственно коммутации ключей. Будем полагать, что одновременно замкнуты три ключа, которые принадлежат к трем разным плечам. Если замкнуты ключи К1, К2 и К3, то эту комбинацию будем обозначать так: К1, К2, К3. Тогда рассматриваемый порядок коммутации ключей можно записать следующим образом: К1, К2, К3; К2, К3, К4; К3, К4, К5; К4, К5, К6; К5, К6, К1; К6, К1, К2 и далее комбинации повторяются. Нетрудно заметить, что через каждые 6 комбинаций происходит повторение порядка коммутации ключей.
. Следовательно, ключи могут работать автономно. Рассмотрим простейший способ подачи управляющих напряжений и соответственно коммутации ключей. Будем полагать, что одновременно замкнуты три ключа, которые принадлежат к трем разным плечам. Если замкнуты ключи К1, К2 и К3, то эту комбинацию будем обозначать так: К1, К2, К3. Тогда рассматриваемый порядок коммутации ключей можно записать следующим образом: К1, К2, К3; К2, К3, К4; К3, К4, К5; К4, К5, К6; К5, К6, К1; К6, К1, К2 и далее комбинации повторяются. Нетрудно заметить, что через каждые 6 комбинаций происходит повторение порядка коммутации ключей.
Будем полагать, что каждая комбинация имеет длительность 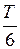 . Тогда полный период изменения всех 6 комбинаций будет равен
. Тогда полный период изменения всех 6 комбинаций будет равен 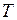 .
.
Заметим, что существует большое разнообразие порядка коммутации ключа. Однако при этом следует помнить о том, что имеются недопустимые комбинации, например, одновременно не могут быть включены или выключены ключи одного плеча. Остальные же комбинации включения или выключения ключей возможны.
Для пояснения принципа действия трехфазного АИН построим временные диаграммы следующих напряжений: 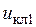 ,
, 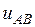 ,
, 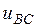 ,
, 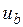 (см. рис. 1), где
(см. рис. 1), где 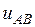 ,
, 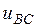 – линейные статорные напряжения;
– линейные статорные напряжения; 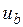 – фазное напряжение фазы В.
– фазное напряжение фазы В.
Построение диаграмм произведем при следующих допущениях. Будем полагать, во-первых, что статорные обмотки соединены в звезду; во-вторых, что при работе двигателя в номинальном (или близком к номинальному) режиме можно считать, что сопротивления статорных обмоток имеют активных характер. Покажем справедливость второго допущения. Для этого рассмотрим схему замещения асинхронного двигателя, приведенную на рис. 2.
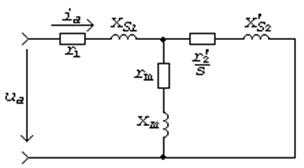
Рис. 2. Схема замещения асинхронного двигателя
На рис. 2 приняты следующие обозначения:  – активное сопротивление статорных обмоток;
– активное сопротивление статорных обмоток; 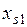 – индуктивное сопротивление рассеивания статорных обмоток;
– индуктивное сопротивление рассеивания статорных обмоток; 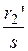 – приведенное активное сопротивление роторных обмоток;
– приведенное активное сопротивление роторных обмоток; 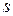 – скольжение;
– скольжение; 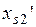 – приведенное индуктивное сопротивление рассеивания обмоток ротора;
– приведенное индуктивное сопротивление рассеивания обмоток ротора; 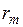 – активное сопротивление контура намагничивания, отражающее потери в стали двигателя;
– активное сопротивление контура намагничивания, отражающее потери в стали двигателя; 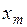 – индуктивное сопротивление контура намагничивания, отражающее намагничивание асинхронного двигателя.
– индуктивное сопротивление контура намагничивания, отражающее намагничивание асинхронного двигателя.
Так как нас интересует только номинальный режим работы двигателя, при котором 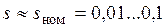 , то для такого режима схема замещения двигателя может быть упрощена в силу следующих соображений.
, то для такого режима схема замещения двигателя может быть упрощена в силу следующих соображений.
Сопротивления  ,
, 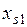 ,
, 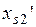 сопоставимы для реальных двигателей. Поэтому величина
сопоставимы для реальных двигателей. Поэтому величина 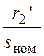 много больше указанных сопротивлений. Сопротивление
много больше указанных сопротивлений. Сопротивление 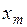 определяет ток холостого хода
определяет ток холостого хода 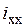 , который составляет
, который составляет 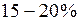 от номинального тока
от номинального тока 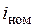 двигателя. Следовательно, при работе двигателя в режиме, близком к номинальному, можно считать, что
двигателя. Следовательно, при работе двигателя в режиме, близком к номинальному, можно считать, что 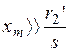 .
.
Исходя из указанных соотношений между сопротивлениями, схема замещения асинхронного двигателя может быть сведена к виду, представленному на рис.3.
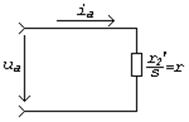
Рис. 3. Упрощенная схема асинхронного двигателя
в номинальном режиме
Теперь можно построить временные диаграммы. Будем рассматривать процессы в течение периода 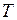 . Временные диаграммы изменения линейных напряжений
. Временные диаграммы изменения линейных напряжений 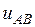 и
и 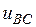 , а также управляющего напряжения
, а также управляющего напряжения 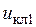 могут быть получены непосредственно из рассмотрения схемы АИН, приведенной на рис. 1.
могут быть получены непосредственно из рассмотрения схемы АИН, приведенной на рис. 1.
Для того чтобы построить временную диаграмму 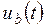 , необходимо предварительно рассмотреть процессы, происходящие в статорных обмотках, соединенных в звезду (см. рис 4). Покажем по результатам такого рассмотрения, что для напряжения
, необходимо предварительно рассмотреть процессы, происходящие в статорных обмотках, соединенных в звезду (см. рис 4). Покажем по результатам такого рассмотрения, что для напряжения 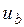 справедливо соотношение:
справедливо соотношение:
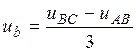 .
.
Для этого выполним следующие преобразования. По 1 закону Кирхгофа для узла запишем:
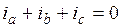 , (1)
, (1)
где 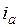 ,
, 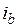 ,
, 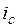 – токи соответственно фаз статора А, В и С.
– токи соответственно фаз статора А, В и С.
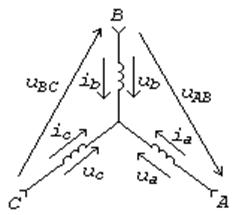
Рис. 4. Схема соединения статорных обмоток
По 2 закону Кирхгофа для фаз A и B запишем (см. рис. 4):
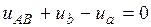 , (2)
, (2)
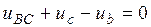 , (3)
, (3)
где 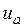 ,
, 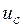 – фазные напряжения статорных обмоток соответственно фаз А и С.
– фазные напряжения статорных обмоток соответственно фаз А и С.
Учитывая схему замещения двигателя (см. рис. 3), по закону Ома запишем:
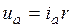 , (4)
, (4)
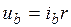 , (5)
, (5)
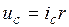 . (6)
. (6)
Выразим из уравнения (2) напряжение 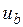 , в результате чего получим
, в результате чего получим
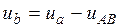 . (7)
. (7)
Из уравнений (4) – (6) выразим токи и подставим полученные для них выражения в уравнение (1). При этом после сокращения  получим
получим
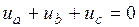 . (8)
. (8)
Из уравнения (3) выразим 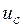 , в результате чего получим
, в результате чего получим
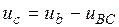 . (9)
. (9)
Подставим теперь уравнение (9) в уравнение (8) и после преобразований получим
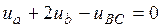 . (10)
. (10)
Из уравнения (10) выразим 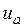 и подставим в уравнение (7). После преобразований получим
и подставим в уравнение (7). После преобразований получим
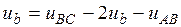 . (11)
. (11)
Откуда следует
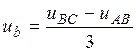 , (12)
, (12)
что и требовалось показать.
Временные диаграммы изменения величин 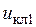 ,
, 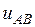 ,
, 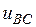 ,
, 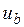 приведены на рис.5. Поясним порядок их построения. Рассмотрим вначале промежуток времени от 0 до
приведены на рис.5. Поясним порядок их построения. Рассмотрим вначале промежуток времени от 0 до 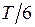 . На этом промежутке ключи К1, К2 и К3, как отмечалось выше, замкнуты. Замыкание и размыкание этих ключей производится соответственно управляющими напряжениями
. На этом промежутке ключи К1, К2 и К3, как отмечалось выше, замкнуты. Замыкание и размыкание этих ключей производится соответственно управляющими напряжениями 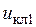 ,
, 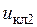 и
и 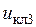 . Будем полагать, что замыкание ключей происходит при высоком положительном уровне указанных управляющих напряжений, а размыкание – при нулевом уровне. С учетом изложенного на первой диаграмме (см. рис. 5) для моментов времени от 0 до
. Будем полагать, что замыкание ключей происходит при высоком положительном уровне указанных управляющих напряжений, а размыкание – при нулевом уровне. С учетом изложенного на первой диаграмме (см. рис. 5) для моментов времени от 0 до 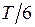 построен график напряжения
построен график напряжения 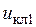 в виде отрезка прямой, удаленного от
в виде отрезка прямой, удаленного от 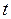 в положительном направлении на некоторое расстояние.
в положительном направлении на некоторое расстояние.
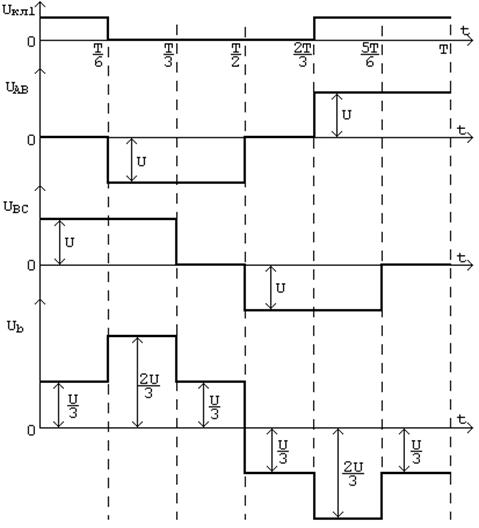
Рис. 5. Временные диаграммы, поясняющие работу АИН
Рассмотрим теперь построение диаграмм напряжений 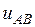 ,
, 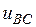 и
и 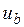 на промежутке времени от 0 до
на промежутке времени от 0 до 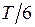 с учетом того, что ключи К1, К2 и К3 замкнуты. В этом случае (см. рис. 1) точка А оказывается на шине (
с учетом того, что ключи К1, К2 и К3 замкнуты. В этом случае (см. рис. 1) точка А оказывается на шине (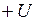 ), точка В – также на шине (
), точка В – также на шине (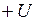 ), а точка С – на шине (
), а точка С – на шине (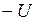 ). Поэтому напряжение
). Поэтому напряжение 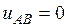 ,
, 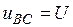 , а фазное напряжение
, а фазное напряжение 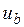 фазы В, как это следует из формулы (12), будет равно
фазы В, как это следует из формулы (12), будет равно 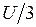 , т.е.
, т.е. 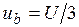 .
.
Рассмотрим далее промежуток времени от 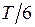 до
до 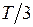 , где замкнуты ключи К2, К3 и К4. Здесь ключ К1 разомкнут и значит управляющее напряжение
, где замкнуты ключи К2, К3 и К4. Здесь ключ К1 разомкнут и значит управляющее напряжение 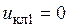 . Для данной комбинации состояния ключей точка А оказывается на шине (
. Для данной комбинации состояния ключей точка А оказывается на шине (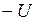 ), точка В – на шине (
), точка В – на шине (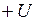 ), а точка С – на шине (
), а точка С – на шине (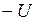 ). Поэтому напряжение
). Поэтому напряжение 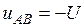 , напряжение
, напряжение 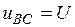 , а фазное напряжение
, а фазное напряжение 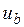 фазы В в силу (12) будет равно
фазы В в силу (12) будет равно 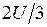 , т.е.
, т.е. 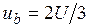 . Далее построение диаграмм осуществляется аналогичным образом.
. Далее построение диаграмм осуществляется аналогичным образом.
Из рис. 5 видно, что, во-первых, 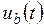 – это некоторая ступенчатая, знакопеременная функция с амплитудой
– это некоторая ступенчатая, знакопеременная функция с амплитудой 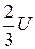 , и, во-вторых, график
, и, во-вторых, график 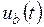 симметричен относительно оси времени, следовательно, постоянная составляющая этого напряжения равна 0. Можно показать, что в напряжении
симметричен относительно оси времени, следовательно, постоянная составляющая этого напряжения равна 0. Можно показать, что в напряжении 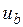 отсутствуют также четные гармоники и гармоники, кратные трем, 5-я гармоника составляет 20% от первой, а 7-я гармоника – 14%. Следует отметить, что существуют и другие комбинации коммутирования ключей, которые снижают уровень высших гармоник.
отсутствуют также четные гармоники и гармоники, кратные трем, 5-я гармоника составляет 20% от первой, а 7-я гармоника – 14%. Следует отметить, что существуют и другие комбинации коммутирования ключей, которые снижают уровень высших гармоник.
Из полученных диаграмм можно сделать также следующие выводы:
· период работы ключа К1 равен 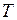 и, следовательно, частота
и, следовательно, частота 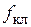 ключа К1 задается равенством
ключа К1 задается равенством
 ; (13)
; (13)
Можно показать, что частоты работы остальных ключей оцениваются аналогично;
· период работы ключа К1 совпадает с периодами напряжений 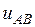 ,
, 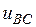 и
и 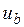 , а, следовательно, для частот
, а, следовательно, для частот 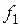 указанных напряжений справедливо
указанных напряжений справедливо
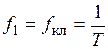 ; (14)
; (14)
Можно показать, что частоты всех выходных напряжений и токов АИН также задается формулой (14).
· амплитуда рассмотренных напряжений, в том числе и фазного, пропорциональна входному постоянному напряжению 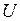 АИН; можно показать, что действующее фазное напряжение
АИН; можно показать, что действующее фазное напряжение 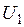 каждой фазы задается равенством
каждой фазы задается равенством
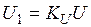 ; (15)
; (15)
· линейные напряжения 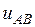 и
и 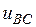 сдвинуты на треть периода
сдвинуты на треть периода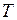 , т.е. на
, т.е. на 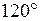 ; можно показать, что все линейные и фазные напряжения сдвинуты на
; можно показать, что все линейные и фазные напряжения сдвинуты на 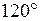 .
.
Из изложенного, таким образом, следует, что линейные и фазные напряжения на выходе АИН представляют собой симметричные трехфазные системы напряжений с частотой 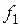 , равной частоте
, равной частоте 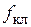 коммутации ключей АИН, а их действующие значения прямо пропорциональны постоянному входному напряжению
коммутации ключей АИН, а их действующие значения прямо пропорциональны постоянному входному напряжению 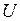 АИН. Это означает, что для регулирования частоты и действующих значений статорных напряжений необходимо изменять соответственно частоту коммутации ключей и входное напряжение
АИН. Это означает, что для регулирования частоты и действующих значений статорных напряжений необходимо изменять соответственно частоту коммутации ключей и входное напряжение 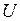 АИН. Такое регулирование может быть как независимым, так и связанным требуемой зависимостью.
АИН. Такое регулирование может быть как независимым, так и связанным требуемой зависимостью.
С учетом изложенного, функциональная схема ПЧН принимает вид, изображенный на рисунке 6.
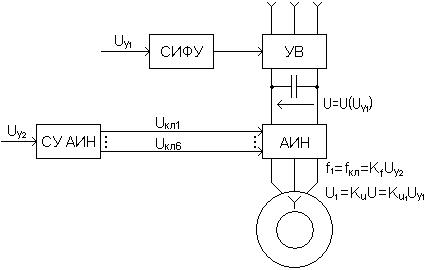
Рис. 6. Функциональная схема ПЧН с независимым регулированием
частоты 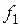 и фазного напряжения
и фазного напряжения 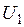
Здесь 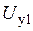 – напряжение, управляющее действующим фазным напряжением
– напряжение, управляющее действующим фазным напряжением 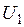 , а
, а 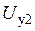 – напряжение, управляющее частотой
– напряжение, управляющее частотой 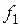 статорных напряжений. В частном случае, когда требуется взаимное регулирование величин
статорных напряжений. В частном случае, когда требуется взаимное регулирование величин 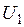 и
и 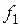 , напряжения
, напряжения 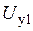 и
и 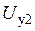 должны быть равны, а требуемая функция связи величин
должны быть равны, а требуемая функция связи величин 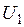 и
и 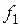 должна задаваться функциональным преобразователем ФП. В этом случае на входы ФП и схемы управления АИН (СУ АИН) подается один и тот же управляющий сигнал
должна задаваться функциональным преобразователем ФП. В этом случае на входы ФП и схемы управления АИН (СУ АИН) подается один и тот же управляющий сигнал 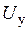 (см. рис. 7).
(см. рис. 7).
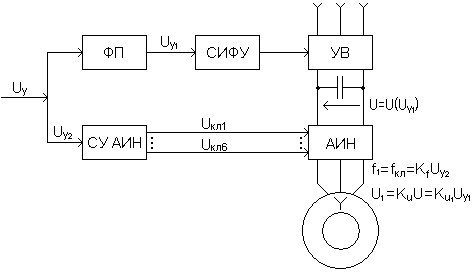
Рис. 7. Функциональная схема ПЧН с зависимым регулированием
частоты 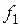 и фазного напряжения
и фазного напряжения 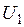
Зная требуемый закон связи величин 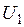 и
и 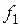 , например, полагая,что он задается в виде закона Костенко
, например, полагая,что он задается в виде закона Костенко
 , (16)
, (16)
можно определить функцию преобразования 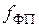 , которая должна связывать выходное напряжение
, которая должна связывать выходное напряжение 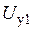 и входное напряжение
и входное напряжение 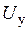 напряжения ФП. Действительно, пусть
напряжения ФП. Действительно, пусть
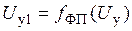 . (17)
. (17)
Из рис. 7 следует
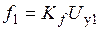 , (18)
, (18)
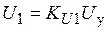 (19)
(19)
Тогда из (16) – (19) следует, что
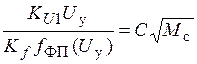 . (20)
. (20)
Откуда
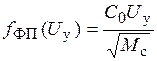 , (21)
, (21)
где 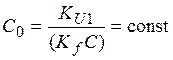 .
.
Из (21) видно, что в рассматриваемом случае ФП задает функциональное преобразование, зависящее от свойств нагрузки, т.е. от момента сопротивления 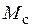 , и от коэффициентов передачи по каналу регулирования напряжения (
, и от коэффициентов передачи по каналу регулирования напряжения (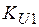 ) и по каналу регулирования частоты (
) и по каналу регулирования частоты (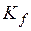 ).
).
В случае, если 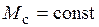 , соотношение (21) показывает, что ФП есть пропорциональное звено с коэффициентом передачи
, соотношение (21) показывает, что ФП есть пропорциональное звено с коэффициентом передачи 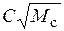 .
.
САМОСТОЯТЕЛЬНО следует найти вид функциональной зависимости 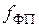 для вентиляторной нагрузки.
для вентиляторной нагрузки.
Статические ПЧН на основе НВ и АИН. Функциональная схема ПЧН, рассматриваемого типа, приведена на рисунке 1. Данные ПЧН состоят из неуправляемого выпрямителя (НВ), автономного инвертора напряжения (АИН) и широтно-импульсного модулятора (ШИМ).
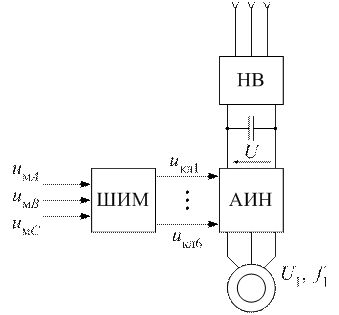
Рисунок 1 – Функциональная схема преобразователя
Неуправляемый выпрямитель предназначен для формирования постоянного напряжения 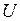 , подводимого к АИН. НВ подключается к трехфазной сети (может использоваться также и однофазная сеть). Конденсатор обеспечивает фильтрацию высших гармоник выходного напряжения НВ.
, подводимого к АИН. НВ подключается к трехфазной сети (может использоваться также и однофазная сеть). Конденсатор обеспечивает фильтрацию высших гармоник выходного напряжения НВ.
ШИМ предназначен для управления ключами АИН. На вход ШИМ подается система модулирующих напряжений 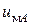 ,
, 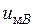 ,
, 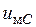 . При этом предполагается, что каждое из модулирующих напряжений имеет амплитуду
. При этом предполагается, что каждое из модулирующих напряжений имеет амплитуду 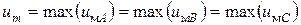 и частоту
и частоту 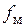 .
.
Выход ШИМ — это шесть напряжений 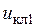 , …,
, …, 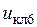 , непосредственно управляющих ключами АИН. Параметры модулирующих напряжений
, непосредственно управляющих ключами АИН. Параметры модулирующих напряжений 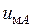 ,
, 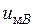 и
и 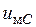 (
(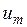 и
и  ) определяют параметры напряжений
) определяют параметры напряжений 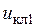 , …,
, …, 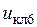 , управляющих ключами, что и позволяет с помощью системы модулирующих напряжений управлять ключами АИН.
, управляющих ключами, что и позволяет с помощью системы модулирующих напряжений управлять ключами АИН.
АИН предназначен для создания трехфазной системы напряжений, параметры которых зависят от параметров модулирующих напряжений. АИН создает в каждой фазе статора АД соответствующее фазное напряжение с действующим значением 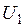 и с частотой
и с частотой 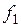 .
.
Величина 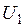 , как это будет показано далее, является функцией амплитуды
, как это будет показано далее, является функцией амплитуды 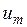 модулирующих напряжений, а частота
модулирующих напряжений, а частота 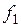 равна частоте
равна частоте 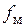 , т.е.
, т.е.
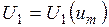 , (1)
, (1)
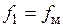 . (2)
. (2)
Это означает, что, изменяя амплитуду 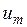 и частоту
и частоту 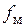 модулирующих напряжений, можно регулировать соответственно действующее значение
модулирующих напряжений, можно регулировать соответственно действующее значение 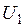 и частоту
и частоту 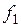 статорных напряжений.
статорных напряжений.
Заметим, что модулирующие напряжения — это напряжения малой мощности, вырабатываемые управляющим устройством, а фазные статорные напряжения, как это будет показано далее, представляют собой напряжения большой мощности. Таким образом, рассматриваемый ПЧН позволяет с помощью маломощного управляющего устройства управлять мощным АД.
Поясним более подробно работу ПЧН с помощью временных диаграмм изменения ряда напряжений этого преобразователя. Для достижений этой цели рассмотрим вначале функциональную схему ШИМ, которая приведена на рисунке 2. ШИМ состоит из генератора несущего напряжений (ГНН) с выходным напряжением 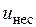 , вычитателей несущего и модулирующих напряжений, компараторов и инверторов.
, вычитателей несущего и модулирующих напряжений, компараторов и инверторов.
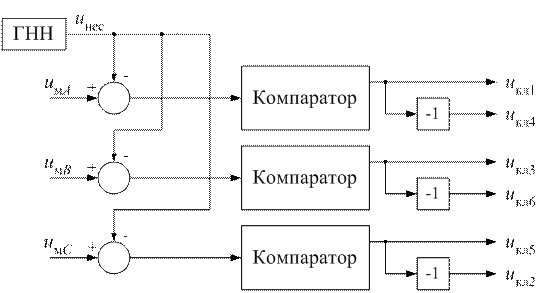
Рисунок 2 – Функциональная схема ШИМ
Сигналы с выходов вычитателей подаются на компараторы. Компаратор — это устройство, на выходе которого сигнал принимает два значения. Значение сигнала на выходе компаратора изменяется при условии, что напряжение на входе переходит через ноль. Выходные напряжения компараторов 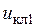 ,
, 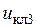 ,
, 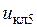 , а также преобразованные через инверторы напряжения
, а также преобразованные через инверторы напряжения 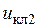 ,
, 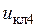 и
и 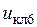 управляют ключами АИН. Каждый компаратор управляет двумя ключами, находящимися в одном плече моста.
управляют ключами АИН. Каждый компаратор управляет двумя ключами, находящимися в одном плече моста.
Будем полагать, что несущее напряжение 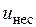 (см. рис. 3, а) имеет треугольную форму. Частота
(см. рис. 3, а) имеет треугольную форму. Частота 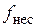 и период
и период 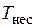 несущего напряжения связаны, очевидно, следующим соотношением
несущего напряжения связаны, очевидно, следующим соотношением
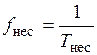 .
.
Несущая частота много больше частоты модулирующих сигналов, т.е. 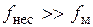 . Будем считать в рассматриваемом ниже примере, что
. Будем считать в рассматриваемом ниже примере, что
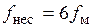 .
.
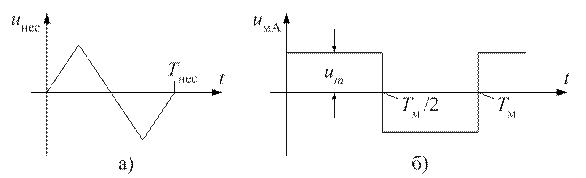
Рисунок 3 – Временные диаграммы несущего 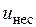 и модулирующего напряжения
и модулирующего напряжения 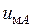 фазы
фазы 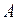
Будем полагать, что модулирующее напряжение для фазы 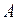 имеет прямоугольную форму (см. рис. 3, б). Будем полагать, что модулирующие напряжения фаз
имеет прямоугольную форму (см. рис. 3, б). Будем полагать, что модулирующие напряжения фаз 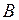 и
и 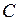 также имеют прямоугольную форму, но сдвинуты по отношению к модулирующему напряжению фазы
также имеют прямоугольную форму, но сдвинуты по отношению к модулирующему напряжению фазы 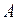 соответственно на треть и две третьих периода
соответственно на треть и две третьих периода 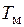 .
.
Кроме того, будем считать, что для периодов модулирующих и несущего напряжений выполняется условие 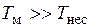 . В частности, в рассматриваемом ниже примере будем считать, что
. В частности, в рассматриваемом ниже примере будем считать, что 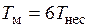 .
.
Перед построением диаграмм укажем также схему АИН (см. рис. 4). Состав элементов этой схемы, порядок их соединения, а также принцип работы были рассмотрены ранее.
Перейдем к построению временных диаграмм, ограничившись диаграммами модулирующих напряжений 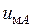 и
и 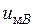 , несущего напряжения
, несущего напряжения 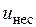 и линейного напряжения
и линейного напряжения 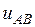 (см. рис. 4). Линейные напряжения
(см. рис. 4). Линейные напряжения 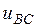 и
и 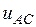 могут быть построены аналогично построению напряжения
могут быть построены аналогично построению напряжения 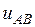 . Заметим, что для построения напряжения
. Заметим, что для построения напряжения 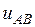 необходимо построить промежуточные диаграммы напряжений
необходимо построить промежуточные диаграммы напряжений 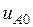 и
и 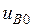 (см. рис. 4).
(см. рис. 4).
При построении временных диаграмм следует учитывать, что амплитуда модулирующих напряжений должна быть меньше амплитуды несущего напряжения.
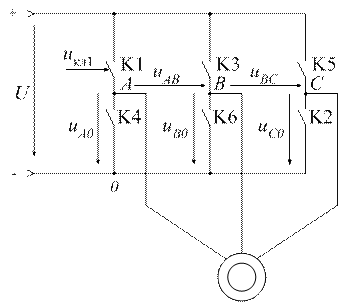
Рисунок 4 – Схема АИН
При построении напряжений 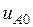 и
и 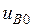 будем считать, что если
будем считать, что если 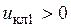 , то ключ К1 замкнут, если
, то ключ К1 замкнут, если 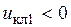 , то ключ К1 разомкнут. Аналогичные предположения примем и относительно других ключей.
, то ключ К1 разомкнут. Аналогичные предположения примем и относительно других ключей.
Определим вначале напряжение 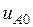 для моментов времени от 0 до
для моментов времени от 0 до 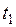 (см. рис. 5), т.е. пока
(см. рис. 5), т.е. пока  . Согласно схеме ШИМ (рисунок 2) получим, что в таком случае
. Согласно схеме ШИМ (рисунок 2) получим, что в таком случае 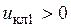 , так как
, так как 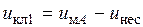 . Так как
. Так как 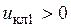 , то ключ К1 замкнут. Вспоминая, что ключи К1 и К4 работают в противофазе, приходим к выводу, что ключ К4 разомкнут. Таким образом, как это видно из рис. 4, напряжение
, то ключ К1 замкнут. Вспоминая, что ключи К1 и К4 работают в противофазе, приходим к выводу, что ключ К4 разомкнут. Таким образом, как это видно из рис. 4, напряжение 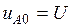 .
.
Оценим далее напряжение 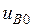 . Так как напряжение
. Так как напряжение 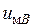 сдвинуто по оси времени относительно
сдвинуто по оси времени относительно 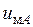 на треть периода
на треть периода 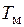 (см. рис. 5), то в рассматриваемые моменты времени
(см. рис. 5), то в рассматриваемые моменты времени 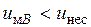 . Поэтому
. Поэтому 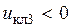 и, следовательно, ключ К3 разомкнут. При этом ключ К6 замкнут, т.к. он работает в противофазе с ключом К3, и, следовательно, как это видно из рис.4, напряжение
и, следовательно, ключ К3 разомкнут. При этом ключ К6 замкнут, т.к. он работает в противофазе с ключом К3, и, следовательно, как это видно из рис.4, напряжение 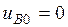 .
.
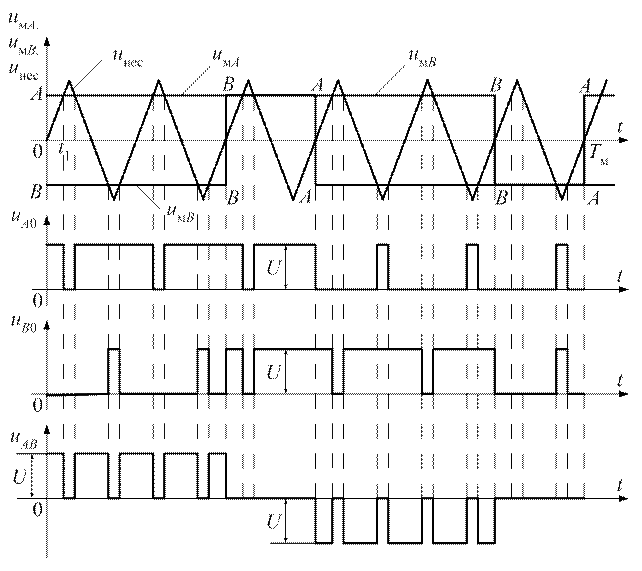 Рисунок 5 – Временные диаграммы напряжений
Рисунок 5 – Временные диаграммы напряжений 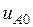 ,
, 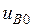 и
и 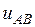
Линейное напряжение 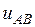 определим по второму закону Кирхгофа (см. рис. 4). Обходя контур, составленный из точек
определим по второму закону Кирхгофа (см. рис. 4). Обходя контур, составленный из точек 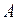 ,
, 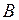 и 0, получаем
и 0, получаем
 .
.
Откуда
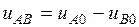 . (3)
. (3)
Опираясь на последнее равенство, нетрудно установить, что для моментов времени от 0 до 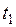
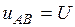 ,
,
что и отражено на нижней диаграмме (см. рис. 5).
Рассуждая аналогично, можно получить временные диаграммы для всего периода 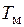 (см. рис. 5).
(см. рис. 5).
Можно показать, что напряжения 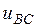 и
и 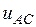 имеют тот же вид, что и напряжение
имеют тот же вид, что и напряжение 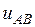 , но сдвинуты относительно напряжения
, но сдвинуты относительно напряжения 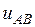 по оси времени соответственно на
по оси времени соответственно на 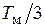 и
и 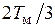 .
.
Из диаграммы, представленной на рис. 5, видно, что напряжение 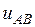 — периодическая функция с нулевым средним значением и периодом
— периодическая функция с нулевым средним значением и периодом 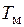 . Следовательно, частота
. Следовательно, частота 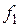 первой гармоники напряжения
первой гармоники напряжения 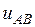 определяется соотношением
определяется соотношением
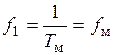 .
.
Покажем, что, изменяя амплитуду модулирующих напряжений 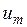 , можно изменять действующее значение
, можно изменять действующее значение 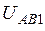 первой гармоники линейного напряжения
первой гармоники линейного напряжения 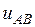 , т.е. покажем, что
, т.е. покажем, что 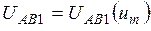 . Пусть
. Пусть 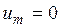 . Тогда
. Тогда 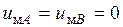 , т.е. модулирующие сигналы одинаковы, а значит одинаковы и напряжения
, т.е. модулирующие сигналы одинаковы, а значит одинаковы и напряжения 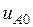 и
и 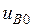 , т.е.
, т.е. 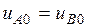 в любой момент времени. Следовательно, в силу равенства (3) приходим к выводу, что
в любой момент времени. Следовательно, в силу равенства (3) приходим к выводу, что
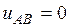
в любой момент времени при 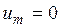 , а значит и действующее значение
, а значит и действующее значение 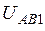 первой гармоники линейного напряжения
первой гармоники линейного напряжения 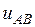 также равно нулю, т.е.
также равно нулю, т.е.
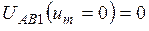 .
.
Из диаграммы (см. рис. 5) видно, что увеличение амплитуды 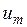 ведет к сужению нулевых промежутков в напряжениях
ведет к сужению нулевых промежутков в напряжениях 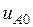 и
и 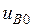 . Это означает, что в них увеличиваются первые гармоники и соответственно увеличивается первая гармоника
. Это означает, что в них увеличиваются первые гармоники и соответственно увеличивается первая гармоника 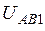 напряжения
напряжения 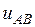 . Изложенное и показывает, что величины
. Изложенное и показывает, что величины 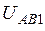 и
и 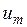 связаны некоторой зависимостью
связаны некоторой зависимостью
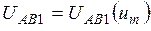 ,
,
монотонно возрастающей от нуля при увеличении амплитуды 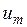 также от нуля.
также от нуля.
Аналогичные выводы по частоте и действующему значению первых гармоник можно сделать и для линейных напряжений 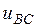 и
и 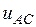 .
.
Построение диаграмм статорных фазных напряжений можно осуществить по диаграммам линейных напряжений так, как это было выполнено в предыдущем параграфе, где рассматривался ПЧН на основе УВ и АИН. В результате этих построений можно, во-первых, установить, что статорные фазные напряжения представляют собой периодические функции с периодом 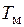 , а, следовательно, и частотой
, а, следовательно, и частотой 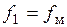 .
.
Во-вторых, можно показать, что статорные фазные напряжения сдвинуты друг относительно друга на величину 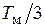 и имеют одинаковые амплитуды, т.е. представляют собой трехфазную симметричную систему напряжений.
и имеют одинаковые амплитуды, т.е. представляют собой трехфазную симметричную систему напряжений.
В-третьих, можно показать, как и для линейных напряжений, что действующее значение 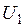 статорных фазных напряжений монотонно увеличивается от нуля при увеличении от нуля амплитуды
статорных фазных напряжений монотонно увеличивается от нуля при увеличении от нуля амплитуды 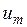 модулирующих напряжений. Это означает, что связь величин
модулирующих напряжений. Это означает, что связь величин 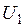 и
и 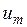 можно представить в виде монотонно возрастающей функции
можно представить в виде монотонно возрастающей функции
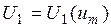 ,
,
обладающей следующим свойством: 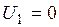 при
при 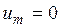 .
.
Сформулируем основные выводы по работе ПЧН с ШИМ:
1. Частота 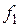 фазных статорных напряжений равна частоте
фазных статорных напряжений равна частоте 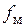 модулирующих напряжений (
модулирующих напряжений (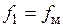 ).
).
2. Действующие значения первых гармоник фазных напряжений зависят от амплитуды модулирующих напряжений, т.е. 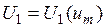 .
.
3. Регулирование частоты 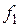 фазных статорных напряжений можно осуществлять путем изменения частоты
фазных статорных напряжений можно осуществлять путем изменения частоты 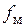 модулирующих напряжений, а регулирование действующих значений фазных статорных напряжений
модулирующих напряжений, а регулирование действующих значений фазных статорных напряжений 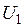 – путем изменения амплитуды
– путем изменения амплитуды 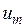 модулирующих напряжений. Причем можно осуществлять как независимое регулирование величин
модулирующих напряжений. Причем можно осуществлять как независимое регулирование величин 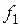 и
и 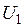 , так и взаимосвязанное, например, по закону Костенко.
, так и взаимосвязанное, например, по закону Костенко.
4. ПЧН с ШИМ представляет собой преобразователь трехфазной системы маломощных модулирующих напряжений в трехфазную систему силовых напряжений. Если модулирующие напряжения имеют прямоугольную форму, то такой ПЧН называют ПЧН с прямоугольной ШИМ. Если модулирующие напряжения изменяются по синусоидальному закону, то ПЧН называется ПЧН с синусоидальной ШИМ. Можно показать, что если синусоидальные модулирующие напряжения изменяются по законам
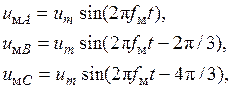 (1)
(1)
то трехфазная система силовых напряжений задается соотношениями
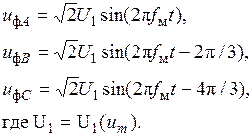 (2)
(2)
Можно показать также, что переход от прямоугольной широтно-импульсной модуляции к синусоидальной снижает уровень высших гармоник статорных напряжений. Соотношения (1) и (2) отражены схемой на рисунке 1. В настоящее время промышленность выпускает, как правило, ПЧН на основе НВ и АИН с синусоидальной ШИМ.
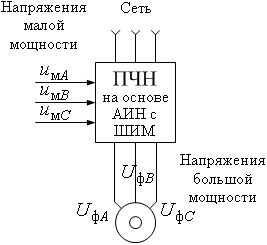
Рисунок 2 – Функциональная схема ПЧН на основе АИН с ШИМ, обеспечивающего преобразование маломощной трехфазной системы напряжений в трехфазную систему напряжений большой мощности
В ПЧН, кроме АИН, могут использоваться автономные инверторы тока (АИТ). Напомним, что АИТ представляют собой преобразователи постоянного напряжения в переменное, обладающие свойствами источника тока. АИТ можно получить на основе АИН двумя способами. Первый способ поясняется рисунком 3. Здесь показано, что в цепь между НВ и АИН включается дроссель, обеспечивающий выходным цепям АИН свойства источника тока.
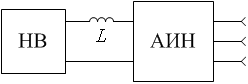
Рисунок 3 – Функциональная схема АИТ с дросселем
Реализация второго способа поясняется рисунком 4. В этом способе организуются обратные связи по фазным статорным токам. Схема содержит три контура регулирования фазных токов 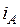 ,
, 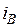 ,
, 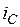 .
.
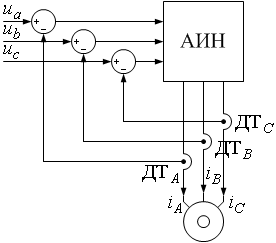
Рисунок 4 – Функциональная схема АИТ с обратными связями:
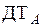 ,
, 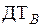 ,
, 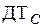 – датчики токов соответственно фаз A, B, C
– датчики токов соответственно фаз A, B, C
Из рисунка видно, что по каждому контуру образуется замкнутая система регулирования фазного тока. Следовательно, в установившемся режиме обеспечивается пропорциональность фазных токов задающим сигналам 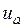 ,
, 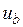 ,
, 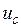 .
.
Можно показать, что АИТ обеспечивает более жесткие механические характеристики электропривода. Это полезно, когда необходимо избавится от обратных связей по угловой скорости. При использовании АИТ управление асинхронным двигателем называется частотно-токовым управлением.
Заканчивая рассмотрение ПЧН, полезно сравнить их технические характеристики с характеристиками ранее рассмотренных ПУ электроприводов постоянного тока.
Таблица 1 – Основные технические характеристики ПУ электроприводов
| масса, кг | объем, л | уд. масса, кг/л | масса, кг | объем, л | уд. масса, кг/л | |
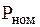
|  кВт кВт
|  кВт кВт
| ||||
| ДПТ | 2,4 | 2,6 | ||||
| УВ | 9,5 | 0,7 | 0,5 | |||
| АД | 2,9 | 2,3 | ||||
| ПЧН | 0,8 |
Из таблицы 1 видно, что максимальные массу и объем при номинальной мощности 1,5 кВт имеет двигатель постоянного тока. Наименьшие показатели при этой же мощности имеет ПЧН. При номинальной мощности 250 кВт максимальные массу и объем имеет асинхронный двигатель, а минимальные – УВ. Следует отметить также, что при изменении номинальной мощности удельные массы рассматриваемых ПУ и двигателей изменяются незначительно. Поэтому средние значения удельных масс могут использоваться при анализе массогабаритных характеристик реальных преобразующих устройств.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1402; Нарушение авторских прав?; Мы поможем в написании вашей работы!