
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вентильный электропривод ЭПБ2
|
|
|
|
Cинхронные электроприводы
Cинхронные электроприводы выполняются на основе синхронных двигателей. Синхронные двигатели имеют высокий коэффициент мощности и высокие значения энергетических характеристик, но по сравнению с другими двигателями имеют более высокую стоимость. Поэтому синхронные электроприводы применяются чаще всего для повышения коэффициента мощности электрических сетей, а также для обеспечения высоких энергетических показателей электроприводов.
Синхронные двигатели делят на:
1) двигатели классической конструкции;
2) вентильные двигатели;
3) бесконтактные двигатели постоянного тока;
4) шаговые двигатели;
5) гистерезисные двигатели;
6) двигатели специальных конструкций.
Наибольшее применение в промышленности нашли приводы с вентильными, бесконтактными и шаговыми двигателями. Рассмотрим вентильный тип электропривода на примере построения привода ЭПБ2.
Вентильный электропривод ЭПБ2имеет следующие основные технические характеристики.
1. Мощность – 400 Вт … 7 кВт.
2. Диапазон регулирования частоты вращения – Д=10 000.
3. Максимальная частота вращения в зависимости от марки двигателя составляет от 1000 об/мин до 4000 об/мин.
4. Погрешность регулирования на максимальной скорости – 0,5%, на минимальной скорости – 25%.
5. Полоса пропускания – 100 Гц.
6. Номинальное напряжение – 500 В, 300 В.
7. Номинальный развиваемый момент – 2,3 … 70 Н·м; мощность при максимальной скорости составляет от 0,75 кВт до 10 кВт.
8. Токи двигателей – 10 … 30 А.
9. Наработка на отказ – 15 000 часов.
10. Используемые марки вентильных двигателей – 2ДВУ115, ДВУ165, 2ДВУ165, ДВУ215, 2ДВУ215; первая цифра 2 в обозначении марки двигателя означает, что ротор двигателя выполнен в виде редкоземельного постоянного магнита, а отсутствие такой цифры означает, что ротор выполнен в виде ферритового постоянного магнита.
11. Масса двигателей – от 5 кг до 75 кг; момент инерции ротора – от 3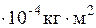 до 330
до 330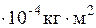 .
.
Поясним вначале конструктивные особенности вентильного двигателя.
Статор вентильного двигателя выполнен по типу статора асинхронного двигателя. На нем уложена трехфазная распределенная обмотка, которая создает трапецеидальное распределение магнитной индукции. Каждая фаза статорной обмотки занимает одну треть поверхности статора, а магнитные оси фаз сдвинуты на 120°. Ротор вентильного двигателя представляет собой постоянный магнит.
В статоре двигателя путем определенного переключения фазных обмоток статора создается вращающееся магнитное поле. Поле ротора взаимодействует с полем статора, вследствие чего ротор вращается за полем статора.
Рассмотрим более детально работу вентильного двигателя. Будем полагать вначале, что включена только фазы А статорной обмотки (см. рис.1). Обмотка этой фазы, как отмечалось выше, занимает одну треть поверхности статора. Будем полагать также, что по обмотке фазы А протекает ток, направление которого отмечено знаками «точка» и «косой крест». Этот ток создает магнитное поле статора, показанное на рис.1 двумя линиями магнитной индукции. На рис.1 показаны также южный S c и северный N c полюсы поля статора при рассматриваемом расположении обмотки фазы А статора и при указанном направлении тока этой обмотки.

Рис.1. Электромагнитная схема вентильного двигателя
Обмотка фазы А статора создает некоторую магнитодвижущую силу (МДС) , которая направлена по магнитной оси этой обмотки от полюса N c к полюсу S c.
, которая направлена по магнитной оси этой обмотки от полюса N c к полюсу S c.
Предположим далее, что ротор (магнит) располагается произвольно, но так, что угол θ (см. рис.1) между продольной магнитной осью ротора и МДС  является острым. Тогда, очевидно, северный полюс N p ротора будет притягиваться к южному полюсу S сстатора, а южный полюс S р ротора – к северному полюсу N с статора. При этом возникнет электромагнитный момент М, действующий по часовой стрелке. Под действием этого момента ротор начнет вращение также по часовой стрелке. Если МДС
является острым. Тогда, очевидно, северный полюс N p ротора будет притягиваться к южному полюсу S сстатора, а южный полюс S р ротора – к северному полюсу N с статора. При этом возникнет электромагнитный момент М, действующий по часовой стрелке. Под действием этого момента ротор начнет вращение также по часовой стрелке. Если МДС 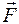 будет оставаться неподвижной, то электромагнитный момент будет действовать по часовой стрелке до тех пор, пока ротор не пройдет положение, при котом θ = 0. После прохождения ротором этого положения электромагнитный момент, очевидно, изменит направление. Поэтому ротор вначале начнет притормаживать, а затем совершать обратное движение к положению, при котором θ = 0. Из изложенного ясно, что ротор будет совершать колебательные движения около положения, при котором θ = 0. Из-за трения эти колебания будут носить затухающий характер и, конечном итоге, ротор остановиться в положении, когда θ = 0. Это положение является равновесным, в силу чего его будем называть устойчивым положением ротора. Заметим, что в устойчивом положении магнитная ось ротора и направление вектора
будет оставаться неподвижной, то электромагнитный момент будет действовать по часовой стрелке до тех пор, пока ротор не пройдет положение, при котом θ = 0. После прохождения ротором этого положения электромагнитный момент, очевидно, изменит направление. Поэтому ротор вначале начнет притормаживать, а затем совершать обратное движение к положению, при котором θ = 0. Из изложенного ясно, что ротор будет совершать колебательные движения около положения, при котором θ = 0. Из-за трения эти колебания будут носить затухающий характер и, конечном итоге, ротор остановиться в положении, когда θ = 0. Это положение является равновесным, в силу чего его будем называть устойчивым положением ротора. Заметим, что в устойчивом положении магнитная ось ротора и направление вектора 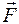 МДС совпадают.
МДС совпадают.
Очевидно, что для дальнейшего вращения ротора по часовой стрелке необходимо, чтобы и МДС 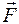 также совершала вращение по часовой стрелке. Такое вращение МДС может быть организовано путем определенной коммутации обмоток статора. Рассмотрим, каковы должны быть оптимальные условия вращения МДС
также совершала вращение по часовой стрелке. Такое вращение МДС может быть организовано путем определенной коммутации обмоток статора. Рассмотрим, каковы должны быть оптимальные условия вращения МДС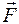 .
.
Для этого остановимся вначале на основных свойствах электромагнитного момента, поскольку его свойства определяют, прежде всего, характеристики вращения ротора. В устойчивом положении ротора, т.е. при θ = 0, электромагнитный момент также равен нулю. В противном случае будет нарушено равновесное состояние ротора.Приходим, таким образом, к выводу, что при θ = 0 электромагнитный момент М = 0.
Заметим далее, что конструкция вентильного двигателя выполнена так, что при других значениях угла θ электромагнитный момент М двигателя в первом приближении может быть определен по следующей формуле:
М = М maxsin θ, (1)
где М max – максимальное значение электромагнитного момента. Из формулы (1) видно, что при θ=900, развиваемый двигателем электромагнитный момент будет максимальным, т.е. М=Мmax.
Из изложенного ясно, что если при θ = 90° начать непрерывное вращение МДС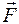 , то также непрерывно начнет вращаться и ротор. Если при этом обеспечивать (какими-либо средствами) выполнение условия θ= 90°, то при вращении ротора на его валу будет действовать максимальный электромагнитный момент. Реализовать данную идею можно, если иметь устройство слежения за углом θ и электронный коммутатор, переключающий обмотки фаз статора по определенному алгоритму. Для реализации устройства слежения за углом θ на ротор устанавливается датчик положения ротора (ДПР). Конструкции разработанных к настоящему времени ДПР весьма разнообразны. ДПР передает значение угла θв электронный коммутатор, который и производит переключение обмоток статора так, чтобы МДС
, то также непрерывно начнет вращаться и ротор. Если при этом обеспечивать (какими-либо средствами) выполнение условия θ= 90°, то при вращении ротора на его валу будет действовать максимальный электромагнитный момент. Реализовать данную идею можно, если иметь устройство слежения за углом θ и электронный коммутатор, переключающий обмотки фаз статора по определенному алгоритму. Для реализации устройства слежения за углом θ на ротор устанавливается датчик положения ротора (ДПР). Конструкции разработанных к настоящему времени ДПР весьма разнообразны. ДПР передает значение угла θв электронный коммутатор, который и производит переключение обмоток статора так, чтобы МДС 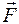 совершала требуемое вращение.
совершала требуемое вращение.
Если электронный коммутатор обеспечивает непрерывное вращение или квазинепрерывное (почти непрерывное) вращение МДС 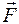 , то такой двигатель называется вентильным. Если электронный коммутатор обеспечивает дискретное (скачкообразное) вращение МДС
, то такой двигатель называется вентильным. Если электронный коммутатор обеспечивает дискретное (скачкообразное) вращение МДС 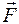 , то такой двигатель называется бесконтактным двигателем постоянного тока.
, то такой двигатель называется бесконтактным двигателем постоянного тока.
Реализовать дискретное вращение существенно проще, чем непрерывное. Но при дискретном вращении МДС 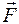 возникают пульсации электромагнитного момента и соответственно частоты вращения ротора. Кроме того, снижается и среднее значение электромагнитного момента, что ухудшает энергетические характеристики машины.
возникают пульсации электромагнитного момента и соответственно частоты вращения ротора. Кроме того, снижается и среднее значение электромагнитного момента, что ухудшает энергетические характеристики машины.
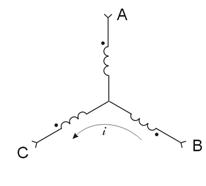
Рассмотрим более детально, каким образом осуществляется управление вращением МДС с помощью электронного коммутатора электропривода ЭПБ2, учитывая, что силовая часть коммутатора выполняется в виде транзисторного автономного инвертора напряжения (см. рис. 2).
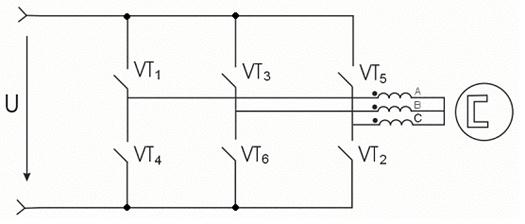
Рис. 2. Функциональная схема включения вентильного двигателя и АИН
В рассматриваемом электроприводе на каждом такте включаются только 2 ключа автономного инвертора напряжения. При этом коммутация ключей осуществляется в следующем порядке:
на 1 такте – VT1, VT2;
на 2 такте – VT3, VT2;
на 3 такте – VT3, VT4;
на 4 такте – VT5, VT4;
на 5 такте – VT5, VT6;
на 6 такте – VT1, VT6.
Рассмотрим процесс вращения МДС обмоток статора. Для этого построим векторные диаграммы расположения МДС, учитывая что продольные магнитные оси обмоток фаз А, В, С статора расположены в пространстве так, как это показано на рис. 3, а. Это, во-первых. Во-вторых, будем полагать для простоты, что обмотки фаз статора имеют одинаковые сопротивления чисто активного характера. Тогда ток i, протекающий по указанным обмоткам будет определяться только входным напряжением U АИН, а также активным сопротивлением обмоток, и не будет зависеть от времени. Это означает, что ток обмоток и, следовательно, МДС всех фаз можно считать неизменными величинами в течение всего периода времени подключения их к АИН. Учитывая сказанное, векторная диаграмма МДС на первом такте работы примет вид, изображенный на рис. 3, б. Прямоугольник, изображенный на этом рисунке, представляет собой ротор, выполненный в виде полосового магнита. На него действует, как это отмечалось выше, электромагнитный момент, который приводит ротор во вращение. Можно показать, что переход к следующему такту нужно произвести при θ=600. Тогда средний электромагнитный момент будет иметь максимальное значение.

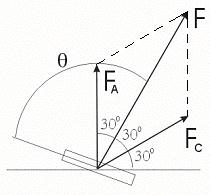
а) б)
Рис. 3. Схема пространственного расположения продольных магнитных осей обмоток фаз А, В и С статора (а) и векторная диаграмма МДС
обмоток статора (б) для первого такта коммутации ключей:
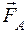 – МДС фазы А статора;
– МДС фазы А статора;  – МДС фазы С статора;
– МДС фазы С статора; 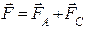 – результирующая МДС обмоток статора
– результирующая МДС обмоток статора
На втором такте к источнику напряжения U подключаются последовательно обмотки фаз С и В. При этом по указанным обмоткам будет протекать один и тот же ток i, который будет создавать МДС  и
и  соответственно фаз В и С статора. Векторные диаграммы указанных МДС, а также результирующей МДС статора имеют вид, представленный на рис. 4, б.
соответственно фаз В и С статора. Векторные диаграммы указанных МДС, а также результирующей МДС статора имеют вид, представленный на рис. 4, б.
Учитывая изложенное, нетрудно показать, что в начале второго такта угол θ=120°. При таком угле силы электромагнитного притяжения будут вращать ротор вслед за результирующей МДС F по часовой стрелке.
Нетрудно видеть, что при указанном алгоритме коммутации транзисторов инвертора результирующая МДС F вращается скачками, что будет вызывать пульсирующий характер движения ротора. Для снижения пульсаций необходимо обеспечить на втором такте (и на всех последующих тактах) широтно-импульсную коммутацию транзисторов, открытых на данном такте. Конкретный вид такой коммутации следует предложить самостоятельно. При этом следует полагать, что ширина импульсов внутри одного такта должна зависеть от угла θ.
Определим далее частоту вращения ротора, а также те факторы, изменяя которые можно изменять частоту вращения ротора. При подключении обмоток статора на источник постоянного напряжения U возникает явление электромагнитной индукции, в результате чего создается ЭДС индукции е в обмотках статора. При этом внешнее напряжение U уравновешивает эту ЭДС е и падение напряжения на активном сопротивлении обмоток.

а) б)
Рис. 4. Схема пространственного расположения продольных магнитных осей обмоток фаз А, В и С статора (а) и векторная диаграмма МДС
обмоток статора (б) для первого такта коммутации ключей:
 – МДС фазы С статора;
– МДС фазы С статора;  – МДС фазы В статора;
– МДС фазы В статора;
 – результирующая МДС обмоток статора
– результирующая МДС обмоток статора
Будем полагать, что падение напряжения на активном сопротивлении равно нулю. Следовательно,
U= е. (2)
Можно показать, что
e = ce Ф ω, (3)
где се – конструктивный коэффициент; Ф – магнитный поток ротора, ω – угловая скорость вращения ротора. Из (2) и (3) следует
U = ce Ф ω. (4)
Откуда
 . (5)
. (5)
Магнитный поток Ф создается постоянным магнитом, следовательно, Ф = const. Причем значение этой константы известно. Поэтому, угловая скорость ω однозначно определяется внешним напряжением U. Это означает, что при регулировании напряжения U можно однозначно регулировать угловую скорость ω.
Для регулирования статорных напряжений в рассматриваемом электроприводе организовано широтно-импульсное управление транзисторами автономного инвертора напряжения.
Изложенный материал представляет собой описание работы силовой части вентильного электропривода ЭПБ2.
В целом ЭПБ2 построен по принципу подчиненного управления. Электропривод содержит две обратные связи: по скорости и по току. Контур тока является внутренним, а контур по скорости – внешним. Оба контура содержат регуляторы скорости и тока соответственно. Контур тока настроен на технический оптимум, а контур скорости – на симметричный оптимум. Регулятор скорости является пропорционально-интегральным регулятором. Он обеспечивает астатические свойства электропривода. Учитывая изложенное, упрощенная функциональная схема вентильного электропривода ЭПБ2 может быть изображена в виде, представленном на рис. 5.
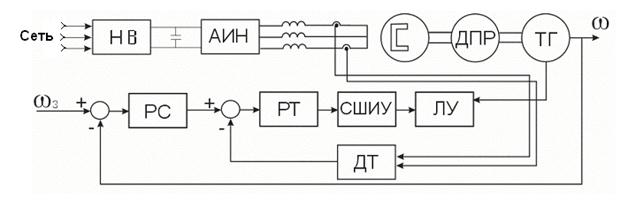
Рис. 5. Упрощенная функциональная схема
вентильного электропривода ЭПБ2:
НВ – неуправляемый выпрямитель; АИН – автономный инвертор напряжения; ДПР – датчик положения ротора; ТГ – тахогенератор; ωз – задающий сигнал по скорости ω; РС – регулятор скорости; РТ – регулятор тока; СШИУ – система широтно-импульсного управления; ЛУ – логическое
устройство; ДТ – датчик токов обмоток статора
3.2.2. Синтез регуляторов вентильных электроприводов
Задача синтеза регуляторов вентильных электроприводов рассматривается в данном параграфе на примере электропривода с двухфазным вентильным двигателем. При использовании трёхфазных вентильных двигателей задача синтеза регуляторов может быть решена аналогично после приведения трёхфазного двигателя к двухфазному.
Для решения задачи синтеза регуляторов требуется динамическая модель двухфазного вентильного двигателя. Ранее, в курсе электрических машин было показано, что двухфазный вентильный двигатель описывается следующей системой дифференциальных уравнений:
 , (3.6)
, (3.6)
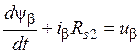 , (3.7)
, (3.7)
 , (3.8)
, (3.8)
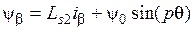 , (3.9)
, (3.9)
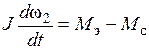 , (3.10)
, (3.10)
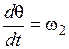 , (3.11)
, (3.11)
 , (3.12)
, (3.12)
где 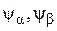 – потокосцепления статорных обмоток
– потокосцепления статорных обмоток  и
и 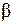 соответственно;
соответственно;  – соответственно токи и напряжения обмоток
– соответственно токи и напряжения обмоток  и
и 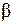 ;
;  – активное сопротивление статорных обмоток
– активное сопротивление статорных обмоток  и
и 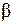 ;
; 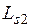 – индуктивность статорных обмоток
– индуктивность статорных обмоток  и
и 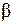 ;
;  – максимальное взаимное потокосцепление обмотки
– максимальное взаимное потокосцепление обмотки  (или
(или 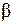 ), обусловленное ротором, выполненным в виде постоянного магнита; p – количество пар полюсов;
), обусловленное ротором, выполненным в виде постоянного магнита; p – количество пар полюсов;  – геометрический угол между продольными магнитными осями ротора и обмотки
– геометрический угол между продольными магнитными осями ротора и обмотки  , отсчитываемый против часовой стрелки от оси обмотки
, отсчитываемый против часовой стрелки от оси обмотки  к оси ротора; J – сумма моментов инерции вала двигателя и приведённого момента инерции нагрузки;
к оси ротора; J – сумма моментов инерции вала двигателя и приведённого момента инерции нагрузки; 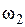 – угловая скорость вращения вала двигателя;
– угловая скорость вращения вала двигателя;  – соответственно электромагнитный (вращающий) момент двигателя и приведённый статический момент сопротивления нагрузки.
– соответственно электромагнитный (вращающий) момент двигателя и приведённый статический момент сопротивления нагрузки.
Непосредственное использование уравнений (3.6) – (3.12) для синтеза регуляторов невозможно. Для решения данной задачи, как и в случае асинхронного двигателя, требуется выполнить преобразование естественных переменных в переменные синхронной системы координат. Будем полагать, что синхронная система координат совпадает с осями d и q, введёнными при рассмотрений вентильного двигателя. Ось d, напомним, направлена по продольной оси ротора, а ось q – по поперечной оси ротора. Тогда следует считать, что
 , (3.13)
, (3.13)
где 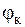 – угол поворота синхронной системы координат. Уравнения координатных преобразований в этом случае приобретают вид:
– угол поворота синхронной системы координат. Уравнения координатных преобразований в этом случае приобретают вид:
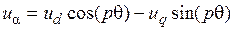 , (3.14)
, (3.14)
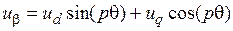 , (3.15)
, (3.15)
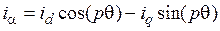 , (3.16)
, (3.16)
 , (3.17)
, (3.17)
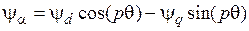 , (3.18)
, (3.18)
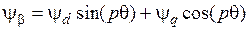 , (3.19)
, (3.19)
где 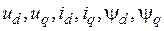 – статорные соответственно напряжения, токи и потокосцепления в синхронной системе координат (d, q).
– статорные соответственно напряжения, токи и потокосцепления в синхронной системе координат (d, q).
Напомним геометрический смысл записанных координатных преобразований на примере преобразований токов 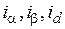 и
и  . Нетрудно показать, что если токи
. Нетрудно показать, что если токи 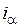 и
и 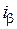 рассматривать как проекции некоторого вектора
рассматривать как проекции некоторого вектора 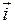 , расположенного под углом
, расположенного под углом 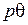 к продольной магнитной оси обмотки
к продольной магнитной оси обмотки  или, иначе говоря, по продольной оси ротора, то в координатах (d, q) этот вектор имеет координаты соответственно
или, иначе говоря, по продольной оси ротора, то в координатах (d, q) этот вектор имеет координаты соответственно  и
и  . Вектор
. Вектор 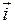 можно рассматривать, очевидно, как МДС некоторой воображаемой обмотки с единичным витком, продольная магнитная ось которой располагается по продольной оси ротора и, следовательно, вращается вместе с ротором.
можно рассматривать, очевидно, как МДС некоторой воображаемой обмотки с единичным витком, продольная магнитная ось которой располагается по продольной оси ротора и, следовательно, вращается вместе с ротором.
Перейдём к подстановке (3.14) – (3.19) в (3.6) – (3.12). Но предварительно вычислим производные  и
и 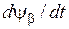 с учетом того, что величины
с учетом того, что величины 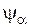 и
и  задаются координатными преобразованиями (3.18) и (3.19). Дифференцируя величины
задаются координатными преобразованиями (3.18) и (3.19). Дифференцируя величины 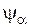 и
и  как сложные функции, получаем:
как сложные функции, получаем:
 (3.20)
(3.20)
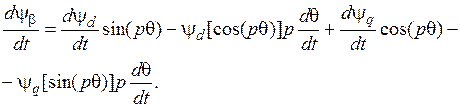 (3.21)
(3.21)
Выполним преобразование равенств (3.6) и (3.7). Подставляя (3.20), (3.14) и (3.16) в (3.6), а также (3.21), (3.15) и (3.17) в (3.7), получаем с учётом замены 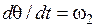 , которая справедлива в силу (3.11), следующую систему уравнений:
, которая справедлива в силу (3.11), следующую систему уравнений:
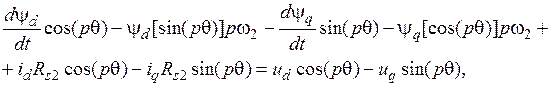 (3.22)
(3.22)
 (3.23)
(3.23)
Выполним преобразование равенств (3.8) и (3.9). Представляя (3.18) и (3.16) в (3.8), а (3.19) и (3.17) в (3.9), получаем:
 , (3.24)
, (3.24)
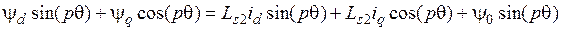 . (3.25)
. (3.25)
Упростим равенства (3.22) и (3.23) следующим образом. Вначале умножим (3.22) на cos(p  ) и (3.23) на sin(p
) и (3.23) на sin(p  ), а затем полученные равенства сложим, в результате чего после преобразований получим, что
), а затем полученные равенства сложим, в результате чего после преобразований получим, что
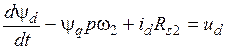 . (3.26)
. (3.26)
Далее умножим (3.22) на [-sin(p  )] и (3.23) на cos(p
)] и (3.23) на cos(p  ), а затем полученные равенства сложим, в результате чего после преобразований получим, что
), а затем полученные равенства сложим, в результате чего после преобразований получим, что
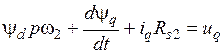 . (3.27)
. (3.27)
Упростим равенства (3.24) и (3.25). Вначале умножим (3.24) на cos(p  ) и (3.25) на sin(p
) и (3.25) на sin(p  ), а затем полученные результаты сложим, в результате чего получим, что
), а затем полученные результаты сложим, в результате чего получим, что
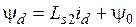 . (3.27а)
. (3.27а)
Далее умножим (3.24) на [- sin(p  )] и (3.25) на cos(p
)] и (3.25) на cos(p  ), а затем полученные равенства сложим, в результате чего получим, что
), а затем полученные равенства сложим, в результате чего получим, что
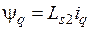 . (3.27б)
. (3.27б)
Итак, после координатных преобразований исходных уравнений (3.6) – (3.9) приходим к уравнениям (3.26) – (3.27б), которые не содержат периодических коэффициентов.
Продолжим преобразование оставшихся исходных уравнений двигателя (3.10) – (3.12). Уравнения (3.10) и (3.11), очевидно, не изменяются координатными преобразованиями, а уравнение (3.12) после подстановки в него (3.16) и (3.17) преобразуется к виду
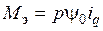 .
.
Таким образом, на основании изложенного приходим к выводу, что уравнения вентильного двигателя в синхронной системе координат имеют следующий вид:
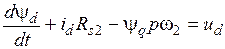 , (3.28)
, (3.28)
 , (3.29)
, (3.29)
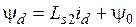 , (3.30)
, (3.30)
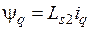 , (3.31)
, (3.31)
 , (3.32)
, (3.32)
 , (3.33)
, (3.33)
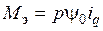 . (3.34)
. (3.34)
Продолжим упрощение уравнений вентильного двигателя. С этой целью в уравнениях (3.28) – (3.34) исключим, во-первых, потокосцепления 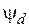 и
и 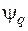 . Во-вторых, будем полагать для простоты, что вентильный электропривод регулирует только угловую скорость
. Во-вторых, будем полагать для простоты, что вентильный электропривод регулирует только угловую скорость 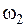 , т.е. не предназначен для регулирования угла
, т.е. не предназначен для регулирования угла  . Тогда из уравнений двигателя может быть исключено уравнение (3.33) для угла
. Тогда из уравнений двигателя может быть исключено уравнение (3.33) для угла  , т.к. эта величина не входит в другие уравнения вентильного двигателя, записанные в синхронных координатах. С учётом изложенного уравнения (3.28) – (3.34) преобразуются к виду:
, т.к. эта величина не входит в другие уравнения вентильного двигателя, записанные в синхронных координатах. С учётом изложенного уравнения (3.28) – (3.34) преобразуются к виду:
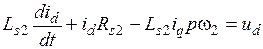 , (3.35)
, (3.35)
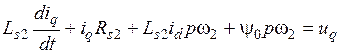 , (3.36)
, (3.36)
 , (3.37)
, (3.37)
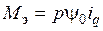 . (3.38)
. (3.38)
Из уравнения (3.38) следует, что электромагнитный момент М э не зависит от тока  , т.е. этот ток не создает полезных усилий на валу двигателя. Ясно, однако, что ток
, т.е. этот ток не создает полезных усилий на валу двигателя. Ясно, однако, что ток  создает электрические потери в обмотках двигателя, протекая по их активным сопротивлениям
создает электрические потери в обмотках двигателя, протекая по их активным сопротивлениям  . Возникает следующая идея: при управлении угловой скоростью
. Возникает следующая идея: при управлении угловой скоростью 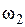 застабилизировать ток
застабилизировать ток  на нулевом уровне, чтобы снизить электрические потери в двигателе.
на нулевом уровне, чтобы снизить электрические потери в двигателе.
Из изложенного, таким образом, следует, что вентильный электропривод должен иметь, по крайней мере, две обратных связи: одну – по угловой скорости 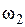 и другую – по току
и другую – по току  . Это означает также, что электропривод должен иметь два задающих устройства. Одно задающее устройство с выходным сигналом
. Это означает также, что электропривод должен иметь два задающих устройства. Одно задающее устройство с выходным сигналом 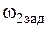 должно определять требуемый закон изменения угловой скорости
должно определять требуемый закон изменения угловой скорости 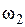 . Другое задающее устройство должно задавать нулевое значение тока
. Другое задающее устройство должно задавать нулевое значение тока  . Это означает, что вырабатываемый этим устройством выходной сигнал
. Это означает, что вырабатываемый этим устройством выходной сигнал  должны быть равен нулю. Итак, приходим к выводу, что для выходного сигнала
должны быть равен нулю. Итак, приходим к выводу, что для выходного сигнала  должно выполнятся равенство
должно выполнятся равенство  =0.
=0.
Построение структурной схемы вентильного электропривода начнем с построения структурной схемы вентильного двигателя, полагая, что угловая скорость 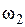 , ток
, ток  и ток
и ток 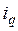 являются выходными сигналами, а напряжения
являются выходными сигналами, а напряжения 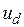 и
и 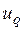 – управляющими сигналами. С этой целью преобразуем уравнения (3.35) – (3.38) к виду:
– управляющими сигналами. С этой целью преобразуем уравнения (3.35) – (3.38) к виду:
 , (3.39)
, (3.39)
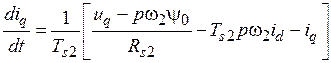 , (3.40)
, (3.40)
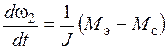 , (3.41)
, (3.41)
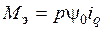 , где
, где  . (3.42)
. (3.42)
Уравнениям (3.39) – (3.42), очевидно, соответствует структурная схема вентильного двухфазного двигателя, приведенная на рис.1.
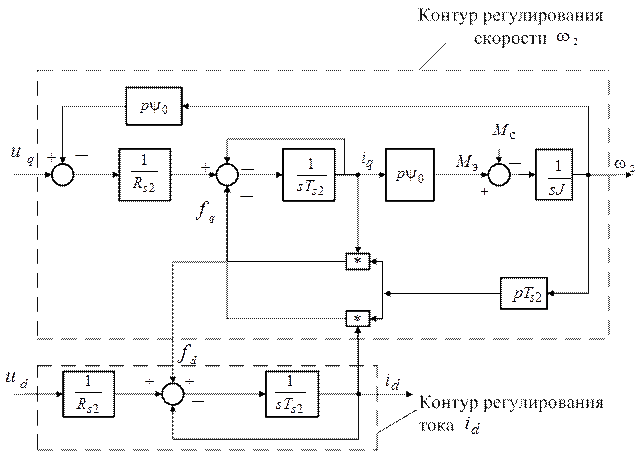
Рис.1. Структурная схема вентильного двухфазного двигателя
в синхронной системе координат
Из этой схемы видно, что на процессы в блоке “Контур регулирования тока  ” влияют переменные
” влияют переменные 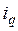 и
и 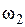 . Величина
. Величина 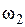 является по сравнению с током
является по сравнению с током  весьма инерционной величиной и поэтому не влияет на переходные процессы в контуре регулирования тока
весьма инерционной величиной и поэтому не влияет на переходные процессы в контуре регулирования тока 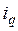 . Если обеспечить медленное изменение тока
. Если обеспечить медленное изменение тока 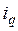 , то ток
, то ток 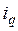 также не будет влиять на динамику контура регулирования тока
также не будет влиять на динамику контура регулирования тока  . Это означает, что в первом приближении при указанных условиях можно считать контур регулирования тока
. Это означает, что в первом приближении при указанных условиях можно считать контур регулирования тока  независимым в динамике от остальной части структурной схемы. Следствием этого свойства является то, что при выборе регулятора тока
независимым в динамике от остальной части структурной схемы. Следствием этого свойства является то, что при выборе регулятора тока  (
( ) можно отбросить возмущающий сигнал
) можно отбросить возмущающий сигнал 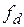 (см. рис.1.)
(см. рис.1.)
Из структурной схемы вентильного двигателя (см.рис.1) видно также, что если ток  =0, то процессы в блоке “Контур регулирования скорости
=0, то процессы в блоке “Контур регулирования скорости 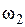 ” не зависят от тока
” не зависят от тока  . Это означает, что при выборе регуляторов для контура регулирования скорости
. Это означает, что при выборе регуляторов для контура регулирования скорости 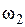 можно отбросить возмущающее воздействие
можно отбросить возмущающее воздействие 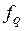 .
.
Приходим, таким образом, к следующему выводу. Для синтеза регуляторов в контуре регулирования тока  можно использовать структурную схему, приведенную на рис.2, а для синтеза регуляторов в контуре регулирования скорости
можно использовать структурную схему, приведенную на рис.2, а для синтеза регуляторов в контуре регулирования скорости 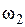 можно использовать структурную схему, приведенную на рис.3.
можно использовать структурную схему, приведенную на рис.3.

Рис.2. Структурная схема вентильного двигателя для выбора регулятора тока  (
(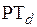 )
)

Рис.3. Структурная схема вентильного двигателя для выбора регулятора угловой скорости 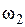 (PC) и регулятора тока
(PC) и регулятора тока  (
( )
)
При определении передаточной функции регулятора тока  (
( ) можно воспользоваться любой известной из теории автоматического управления методикой. В частности, можно воспользоваться методикой настройки на технический или симметричный оптимумы при следующих условиях. Во-первых, следует полагать, что быстродействие системы стабилизации тока
) можно воспользоваться любой известной из теории автоматического управления методикой. В частности, можно воспользоваться методикой настройки на технический или симметричный оптимумы при следующих условиях. Во-первых, следует полагать, что быстродействие системы стабилизации тока  на нулевом уровне должно быть выше, чем длительность переходных процессов по току
на нулевом уровне должно быть выше, чем длительность переходных процессов по току 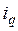 и скорости
и скорости 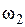 . Во-вторых, следует оценить постоянную времени силового преобразователя, создающего напряжение
. Во-вторых, следует оценить постоянную времени силового преобразователя, создающего напряжение 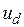 .
.
При определении регуляторов системы управления угловой скоростью 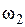 необходимо обратить внимание на следующее. Структурная схема объекта управления, для которого требуется в этом случае выбирать регуляторы представлена, как это отмечалось выше, на рис.3. Эта структурная схема совпадает, по существу, со структурной схемой двигателя постоянного тока с якорным управлением. Следовательно, здесь могут быть применены все идеи и методики подчиненного управления. Нетрудно видеть, что ток
необходимо обратить внимание на следующее. Структурная схема объекта управления, для которого требуется в этом случае выбирать регуляторы представлена, как это отмечалось выше, на рис.3. Эта структурная схема совпадает, по существу, со структурной схемой двигателя постоянного тока с якорным управлением. Следовательно, здесь могут быть применены все идеи и методики подчиненного управления. Нетрудно видеть, что ток 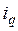 является здесь аналогом якорного тока, а произведение
является здесь аналогом якорного тока, а произведение 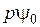 – аналогом противо-ЭДС двигателя постоянного тока. Таким образом, по аналогии с электроприводом постоянного тока с якорным управлением вентильный электропривод должен содержать регулятор скорости (PC) и регулятор тока
– аналогом противо-ЭДС двигателя постоянного тока. Таким образом, по аналогии с электроприводом постоянного тока с якорным управлением вентильный электропривод должен содержать регулятор скорости (PC) и регулятор тока  (
( ).
).
Учитывая изложенное, нетрудно показать, что структурная схема вентильного электропривода в синхронных координатах имеет вид, представленный на рис.4.
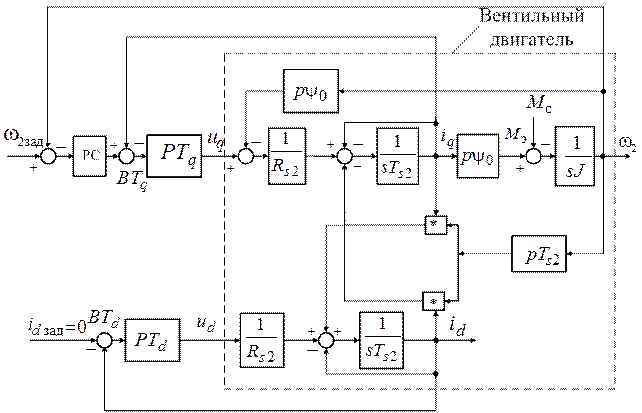
Рис.4. Структурная схема вентильного электропривода
с двухфазным двигателем в синхронных координатах
Заметим, что данная структурная схема предназначена, прежде всего для синтеза регуляторов PC,  , а также для моделирования процессов в вентильном электроприводе с целью уточнения его динамических свойств после выбора указанных регуляторов.
, а также для моделирования процессов в вентильном электроприводе с целью уточнения его динамических свойств после выбора указанных регуляторов.
Для создания реального вентильного электропривода управляющие напряжения 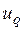 и
и 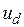 должны быть преобразованы по формулам координатных преобразований в статорные напряжения
должны быть преобразованы по формулам координатных преобразований в статорные напряжения  . Это, во-первых. Во-вторых, для подачи синхронных токов
. Это, во-первых. Во-вторых, для подачи синхронных токов  и
и 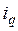 соответственно на выходы вычитателей токов
соответственно на выходы вычитателей токов  (см. рис.4) необходимо их получить из реальных статорных токов
(см. рис.4) необходимо их получить из реальных статорных токов 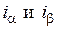 путем координатных преобразований. С учетом изложенного следует самостоятельно построить функциональную схему вентильного электропривода, включающую схему реального вентильного электродвигателя, схемы координатных преобразователей, датчика положения ротора и силовых преобразовательных устройств.
путем координатных преобразований. С учетом изложенного следует самостоятельно построить функциональную схему вентильного электропривода, включающую схему реального вентильного электродвигателя, схемы координатных преобразователей, датчика положения ротора и силовых преобразовательных устройств.
Выбор регуляторов вентильных электроприводов с трехфазными двигателями может быть произведен аналогично после приведения трехфазного вентильного двигателя к двухфазному. Методика такого приведения аналогична рассмотренной в курсе электрических машин методике приведения асинхронных трехфазных двигателей к двухфазным.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 5329; Нарушение авторских прав?; Мы поможем в написании вашей работы!