
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторное управление
|
|
|
|
Управляющие устройства асинхронных электроприводов.
Управление асинхронными электроприводами организуется как по разомкнутому принципу (без обратных связей), так и по замкнутому принципу (с обратными связями).
При управлении асинхронными двигателями с жесткими механическими характеристиками первый способ управления получил достаточно широкое распространение. Но у разомкнутого принципа управления асинхронными двигателями есть следующие недостатки:
1) относительно низкий диапазон регулирования частоты вращения;
2) относительно невысокое быстродействие системы управления;
3) при неизвестном характере зависимости момента сопротивления от частоты вращения (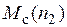 ) оказывается неизвестным закон взаимосвязи
) оказывается неизвестным закон взаимосвязи 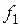 и
и 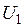 . Это, как известно, может привести к возникновению недопустимо больших статорных токов.
. Это, как известно, может привести к возникновению недопустимо больших статорных токов.
Таким образом, если требуется реализовать систему управления асинхронным электроприводом с большим динамическим диапазоном или высоким быстродействием, или с неизвестной зависимостью 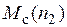 , то необходимо перейти к электроприводу с обратными связями.
, то необходимо перейти к электроприводу с обратными связями.
Основной вопрос при организации управления – реализация управляющего устройства (УУ). При синтезе управляющих устройств могут быть использованы следующие модели АД:
1) статическая модель АД;
2) упрощенная динамическая модель АД;
3) векторная модель АД.
Статическая модель получается из схемы замещения АД (см. рис. 5). На основе этой схемы можно синтезировать УУ.
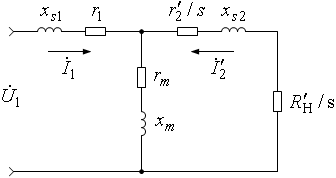
Рисунок 5 – Схема замещения АД
Можно показать, что в качестве упрощенной динамической модели частотно управляемого АД можно использовать передаточную функцию 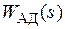 апериодического звена с электромеханической постоянной времени
апериодического звена с электромеханической постоянной времени 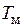 и коэффициентом передачи
и коэффициентом передачи 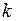 , т.е. можно считать, что
, т.е. можно считать, что
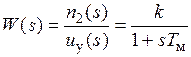 , (3)
, (3)
где 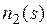 – изображение частоты вращения ротора;
– изображение частоты вращения ротора; 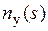 – изображение напряжения, управляющего частотой статорных напряжений.
– изображение напряжения, управляющего частотой статорных напряжений.
Векторная модель представляет собой систему конечно-дифференциальных уравнений, устанавливающих связь между всеми переменными состояния объекта, управляющими факторами и внешними воздействиями. Векторная модель является наиболее точной.
Первые две модели применяются при синтезе УУ в тех случаях, когда не требуется высокое быстродействие системы.
Векторная модель используется при синтезе быстродействующих электроприводов, т.к. в векторной модели наиболее полно учтены динамические свойства АД. Управление АД с использованием ее векторной модели называют векторным управлением.
В настоящее время на основе векторных моделей АД получили распространение УУ с управлением по вектору главного (результирующего) потокосцепления АД, по вектору потокосцепления статора и по вектору потокосцепления ротора. Рассмотрим синтез УУ с управлением по вектору потокосцепления ротора.
Управление асинхронным электроприводом по вектору потокосцепления ротора. Данный тип векторного управления асинхронным электроприводом был впервые использован фирмой «Сименс» в 1971 году [Дартау, Рудаков, с.66,79]. Это управление основывается на векторной модели ТАД, ориентированной по вектору потокосцепления ротора. Такая модель получается из общей модели ТАД, заданной равенствами (95) – (106) в §«Векторные модели асинхронных двигателей» дисциплины «Электромашинные средства автоматизации и управления», при условии, что вектор потокосцепления ротора 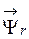 сориентирован по оси х синхронной системы координат (х,у). Тогда
сориентирован по оси х синхронной системы координат (х,у). Тогда
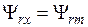 , (1)
, (1)
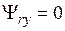 , (2)
, (2)
где  – длина вектора
– длина вектора 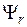 , имеющая смысл максимума потокосцепле-ния ротора.
, имеющая смысл максимума потокосцепле-ния ротора.
При условиях (1) и (2) уравнения (95) – (106) преобразуются к виду:
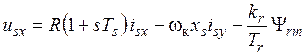 , (3)
, (3)
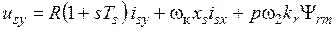 , (4)
, (4)
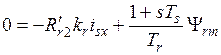 , (5)
, (5)
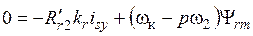 , (6)
, (6)
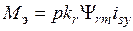 , (7)
, (7)
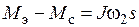 , (8) где s – оператор Лапласа.
, (8) где s – оператор Лапласа.
Рассмотрим возможность регулирования величины 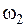 . Для этого определим
. Для этого определим 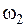 , рассуждая следующим образом. В шести уравнениях (3) – (8) имеется восемь переменных: usx, usy, isx, isy,
, рассуждая следующим образом. В шести уравнениях (3) – (8) имеется восемь переменных: usx, usy, isx, isy,  , ωк, ω2, М э. Величину ω2 можно найти, свернув (3) – (8) в одно уравнение, разрешенное относительно ω2, и исключив при свертывании лишние переменные. Тогда получается функция вида
, ωк, ω2, М э. Величину ω2 можно найти, свернув (3) – (8) в одно уравнение, разрешенное относительно ω2, и исключив при свертывании лишние переменные. Тогда получается функция вида
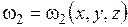 , (9)
, (9)
где х, у, z – какие-либо три переменные из восьми названных выше.
Пусть это будут величины usx, usy и  .
.
Заметим, что величину  желательно стабилизировать так, чтобы машина работала на криволинейном участке магнитной характеристики. Тогда машина будет иметь, как это отмечалось выше, оптимальные массо-габаритные характеристики. Кроме того, машина в этом случае не будет попадать в насыщение, достижение которого приводит к нарушению ее работоспособности, и будет иметь максимально возможный при прочих равных условиях электромагнитный элемент М э, как это видно из (7).
желательно стабилизировать так, чтобы машина работала на криволинейном участке магнитной характеристики. Тогда машина будет иметь, как это отмечалось выше, оптимальные массо-габаритные характеристики. Кроме того, машина в этом случае не будет попадать в насыщение, достижение которого приводит к нарушению ее работоспособности, и будет иметь максимально возможный при прочих равных условиях электромагнитный элемент М э, как это видно из (7).
Для стабилизации величины  необходимо ее измерение. Напомним, что потокосцепление ротора
необходимо ее измерение. Напомним, что потокосцепление ротора  представляет собой сумму основного потокосцепления ротора и потокосцепления рассеяния ротора. В зазоре можно измерить только основное потокосцепление. Это объясняется следующим. Линии магнитной индукции, обуславливающие основное потокосцепление, направлены по радиусу, а линии магнитной индукции, обуславливающие потокосцепление рассеяния, направлены вдоль средней линии воздушного зазора (см. рис.1).
представляет собой сумму основного потокосцепления ротора и потокосцепления рассеяния ротора. В зазоре можно измерить только основное потокосцепление. Это объясняется следующим. Линии магнитной индукции, обуславливающие основное потокосцепление, направлены по радиусу, а линии магнитной индукции, обуславливающие потокосцепление рассеяния, направлены вдоль средней линии воздушного зазора (см. рис.1).
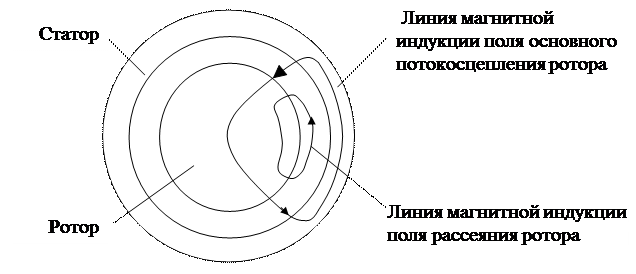
Рис.1. Линии магнитной индукции основного магнитного поля ротора
и поля рассеяния ротора
Если потокосцепление измерять через ЭДС с помощью катушки небольших габаритов, то при расположении плоскостей ее витков на цилиндрических поверхностях ротора или статора линии поля рассеяния будут проскальзывать, как это видно из рис.1, вдоль витков катушки, не наводя в ней ЭДС. При этом линии основного потокосцепления будут пересекать плоскости витков по нормали, наводя в них максимальную ЭДС. Изложенное и поясняет возможность измерения только части потокосцепления ротора  , которая представляет собой основное потокосцепление ротора. Тем не менее полное потокосцепление ротора
, которая представляет собой основное потокосцепление ротора. Тем не менее полное потокосцепление ротора  можно определить по основному, путем расчетов по соотношениям (3.4) из [Рудаков, Дартау, с.68]. Поэтому в дальнейшем будем полагать, что величину
можно определить по основному, путем расчетов по соотношениям (3.4) из [Рудаков, Дартау, с.68]. Поэтому в дальнейшем будем полагать, что величину  можно измерить.
можно измерить.
Итак, основной вывод, который следует из выше изложенного, можно сформулировать так. Разумно систему векторного управления угловой скоростью 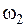 составить из двух подсистем: подсистемы регулирования этой скорости
составить из двух подсистем: подсистемы регулирования этой скорости 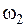 и подсистемы стабилизации амплитуды
и подсистемы стабилизации амплитуды  полного потокосцепления ротора. Для регулировки величины
полного потокосцепления ротора. Для регулировки величины 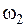 будем использовать напряжение usy, а для стабилизации величины
будем использовать напряжение usy, а для стабилизации величины  – напряжение usx.. Это означает, что изменение напряжения usy должно приводить только к изменению величины
– напряжение usx.. Это означает, что изменение напряжения usy должно приводить только к изменению величины 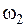 и не должно оказывать никакого влияния на величину
и не должно оказывать никакого влияния на величину  . Аналогично изменение напряжения usx должно приводить только к изменению величины
. Аналогично изменение напряжения usx должно приводить только к изменению величины  и не должно оказывать никакого влияния на величину
и не должно оказывать никакого влияния на величину 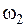 . Однако, как это следует из уравнений (3) – (8),
. Однако, как это следует из уравнений (3) – (8),
изменение напряжения usy приводит к изменению как величины 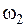 , так и величины
, так и величины  . То же свойство характерно и для напряжения usx. Возникает идея: ввести такую управляющую переменную
. То же свойство характерно и для напряжения usx. Возникает идея: ввести такую управляющую переменную 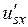 , которая будет влиять только на величину
, которая будет влиять только на величину  , и такую управляющую переменную
, и такую управляющую переменную 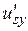 , которая будет влиять только на величину ω2. Для реализации этой идеи введем в (3) – (8) новые управляющие переменные
, которая будет влиять только на величину ω2. Для реализации этой идеи введем в (3) – (8) новые управляющие переменные 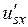 и
и 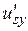 , задаваемые по формулам:
, задаваемые по формулам:
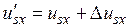 , (10)
, (10)
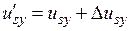 , (11)
, (11)
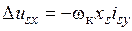 , (12)
, (12)
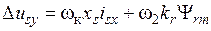 . (13)
. (13)
Тогда уравнения (3) – (6), описывающие ТАД, примут с учетом (10) – (13) вид:
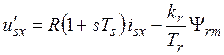 , (14)
, (14)
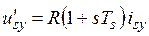 , (15)
, (15)
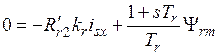 , (16)
, (16)
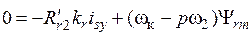 , (17)
, (17)
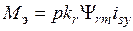 , (18)
, (18)
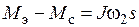 . (19)
. (19)
Из (14) – (19) видно, что в силу равенств (14) и (16) величина 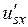 влияет непосредственно только на потокосцепление
влияет непосредственно только на потокосцепление  . Поэтому по этим уравнениям (14) и (16) построим систему стабилизации величины
. Поэтому по этим уравнениям (14) и (16) построим систему стабилизации величины  .
.
Заметим далее, что при
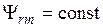 (20)
(20)
величина 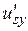 позволяет в силу (15) и (17) регулировать только угловую скорость
позволяет в силу (15) и (17) регулировать только угловую скорость 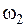 .
.
Выполненные операции (10) – (13) замены управляющих переменных, таким образом, обеспечили получение модели управляемого ТАД с развязанными, т.е. независимыми, каналами регулирования угловой скорости 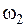 и потокосцепления
и потокосцепления  ротора. Будем называть такую модель ТАД развязанной по каналам регулирования или, коротко, развязанной.
ротора. Будем называть такую модель ТАД развязанной по каналам регулирования или, коротко, развязанной.
Построим структурную схему развязанной модели ТАД и дополним ее регуляторами, необходимыми для регулирования скорости 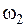 и потокосцепления
и потокосцепления  (см.рис.2). Назовем эту схему регулирующим блоком системы векторного управления.
(см.рис.2). Назовем эту схему регулирующим блоком системы векторного управления.
Регулирование  и
и 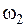 будем производить по схеме подчиненного управления, принимая во внимание следующее. В контур управления
будем производить по схеме подчиненного управления, принимая во внимание следующее. В контур управления  входит ток isx, который является менее инерционной величиной, чем
входит ток isx, который является менее инерционной величиной, чем  . Поэтому введем контур регулирования тока isx в качестве внутреннего по отношению к контуру регулирования потокосцепления
. Поэтому введем контур регулирования тока isx в качестве внутреннего по отношению к контуру регулирования потокосцепления  (см. рис.2). Напомним, что при организации подчиненного управления вводят регуляторы по каждой переменной, т.е. в данном случае следует ввести регуляторы тока isx (РТ х) и потокосцепления ротора
(см. рис.2). Напомним, что при организации подчиненного управления вводят регуляторы по каждой переменной, т.е. в данном случае следует ввести регуляторы тока isx (РТ х) и потокосцепления ротора  (РП). При расчете параметров РТ х отбрасывают обратную связь по
(РП). При расчете параметров РТ х отбрасывают обратную связь по  (через блок kr/Tr), так как величина
(через блок kr/Tr), так как величина  является более инерционной, чем ток isx.
является более инерционной, чем ток isx.
При регулировании скорости 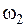 в контур управления входит ток isy, который является менее инерционной величиной, чем скорость
в контур управления входит ток isy, который является менее инерционной величиной, чем скорость 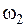 . Поэтому контур регулирования тока isy должен быть внутренним по отношению к контуру регулирования скорости
. Поэтому контур регулирования тока isy должен быть внутренним по отношению к контуру регулирования скорости 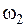 . Для регулировки тока isy вводят регулятор тока (РT у), а для регулировки скорости
. Для регулировки тока isy вводят регулятор тока (РT у), а для регулировки скорости 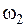 регулятор скорости (РС). При определении параметров РС и РТ у полагают, что
регулятор скорости (РС). При определении параметров РС и РТ у полагают, что  = = const. Это означает, что РП должен обеспечивать быстродействие, большее на порядок, чем быстродействие контура регулирования скорости
= = const. Это означает, что РП должен обеспечивать быстродействие, большее на порядок, чем быстродействие контура регулирования скорости 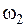 . Тогда контуры регулирования потокосцепления
. Тогда контуры регулирования потокосцепления  и скорости
и скорости 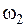 будут развязаны и система в целом будет работать правильно.
будут развязаны и система в целом будет работать правильно.
Для практической реализации системы векторного управления ТАД, структурная схема которой приведена на рис.2, необходимо иметь расчетные величины  , usx, usy, isx, isy.
, usx, usy, isx, isy.
В [Рудаков, Дартау, с.68] показано, что потокосцепление Ψ rm можно определить из соотношения
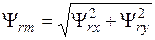 , (21)
, (21)
где величины Ψ rx и Ψ ry определяются путем фазно-координатных преобразований величин Ψ r α и Ψ r β, которые рассчитываются по формулам:
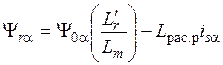 , (22)
, (22)
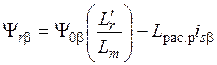 , (23)
, (23)
где Ψ0α, Ψ0β – потокосцепления основного потока ТАД по осям α и β, измеряемые датчиками, которые располагаются на поверхности статора по взаимно перпендикулярным осям α и β; 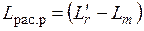 – индуктивность рассеяния обмотки ротора.
– индуктивность рассеяния обмотки ротора.
Вычислительное устройство, реализующее равенства (22) и (23), обозначим BΨ r αβ.
Для нахождения величин usx и usy воспользуемся равенствами (10) – (13). Назовем блок, определяющий величину Δ usx по величинам ωк и isy согласно равенству (12), первым блоком компенсации и обозначим его БК1. Блок, определяющий величину Δ usy по величинам ωк, isy, ω2 и Ψ rm согласно равенству (13), назовем вторым блоком компенсации и обозначим его БК2. Для определения токов isx и isy используем блоки, реализующие фазно-координатные преобразования статорных токов iA, iB, iC.
Воздействие на ТАД будем производить с помощью статорных напряжений uA, uB, uC. Система управления вырабатывает эти напряжения как сигнальные величины, т.е. величины, имеющие малую мощность. Поэтому их нужно усилить по мощности. Для этой цели необходимо использовать автономный инвертор напряжения (АИН) с широтно-импульсной модуляцией (ШИМ), который питается от мощной электроэнергетической сети, а его выходное силовое напряжение повторяет по форме маломощное выходное напряжение (uA, uB, uС) системы уравнения. Таким образом, реальная система векторного управления должна содержать АИН с ШИМ.
Получение маломощных трехфазных напряжений uA, uB, uC может быть произведено путем координатно-фазных преобразований напряжений usx и usy, которые получаются из соотношений (10) и (11).
Частотa ωк находится из (17). Откуда после преобразования следует
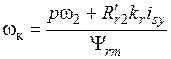 . (24)
. (24)
Назовем блок, вычисляющий величину ωк согласно (24), вычислителем синхронной скорости и обозначим его ВСС.
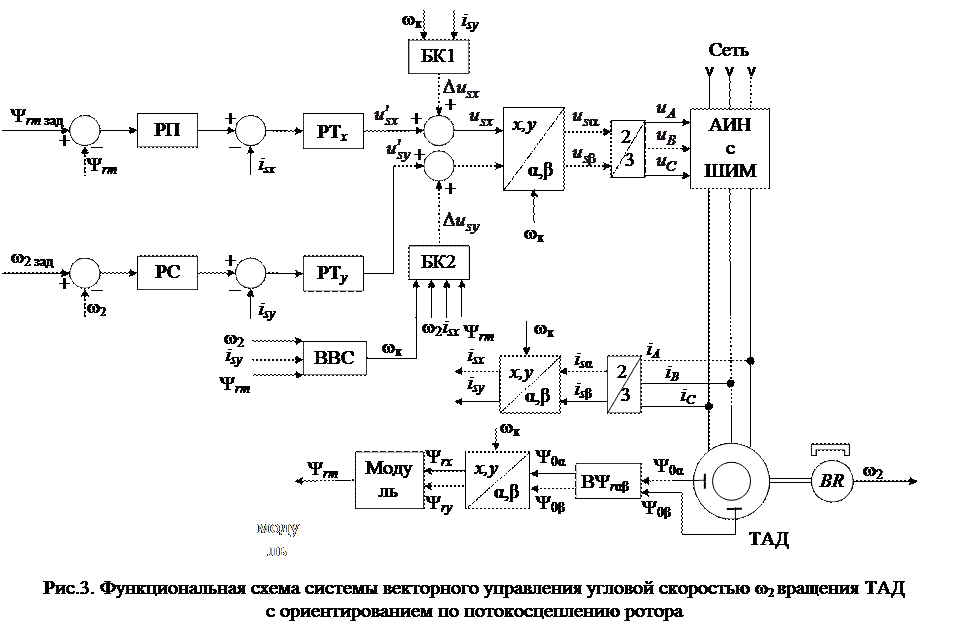
С учетом изложенного на рис.3 приведена функциональная схема системы векторного управления скоростью ТАД с ориентированием по вектору потокосцепления ротора, включающая реальный ТАД и силовой АИН с ШИМ.
|

В заключение отметим следующее.
1. Синтез рассмотренной системы векторного управления скоростью ТАД (или, иначе говоря, асинхронным электроприводом по скорости) проводится, по существу, подобно тому, как это делается в системах подчиненного управления электроприводами постоянного тока при двухзонном регулировании скорости. Динамические характеристики системы векторного управления асинхронным электроприводом аналогичны динамическим характеристикам системы управления электроприводом постоянного тока [Башарин, Упр. ЭП, с. 125].
2. Системы векторного управления асинхронными электроприводами могут быть построены также с ориентированием по векторам потокосцепления статора и главного потокосцепления асинхронного двигателя [Рудаков, с. 5, 92].
3. В качестве силовых преобразователей в асинхронных электроприводах могут быть использованы вместо АИН с ШИМ автономные инверторы тока. Регулирующий блок в этом случае имеет более простую структуру, а механические характеристики асинхронного двигателя оказываются более жесткими [ Герман-Галкин, Комп. моделир., с. 259-263].
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1448; Нарушение авторских прав?; Мы поможем в написании вашей работы!