Геометрическое представление колебаний

Если колебания u_a(t) и u_b(t) представлены в виде рядов Фурье

;

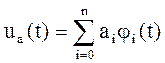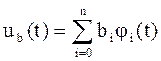
то в n - мерном евклидовом пространстве этим колебаниям можно сопоставить вектора 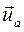и . Модуль каждого из этих векторов соответственно равен

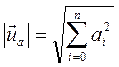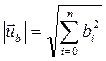; , (2.29)

а расстояние между концами векторов равно (Евклидова метрика)

(2.30)

Эта величина характеризует степень различия между этими 2-мя колебаниями.

В случае двухмерного векторного пространства разностный вектор (расстояние между векторами) равен.

Можно изобразить эти векторы графически рис. 2.11.

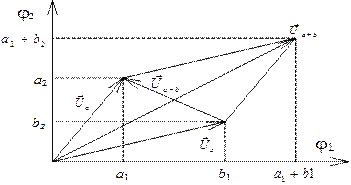
Рис.2.11. Геометрическое представление колебаний.

Спектральная плотность амплитуд (СПА) непериодических сигналов может быть получена из (2.28) при Т→ ∞ и является комплексной функцией частоты, например, для одиночного видеоимпульса рис. 2.10г

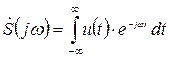, [В/Гц], (2.31)

где обратное преобразование Фурье

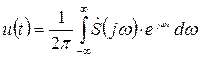(2.32)

Свойства пары преобразования Фурье:

1. Теорема запаздывания для u₂(t)= u₁(t- t_с)

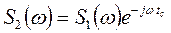(2.33-1)

2. Теорема линейности

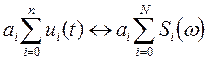(2.33-2)

3. Теорема смещения спектра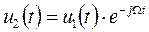

(2.33-3)

4.Изменение масштаба времени, u₂(t)= u₁(bt), b>0 (при b>1 сжатие исходного сигнала)

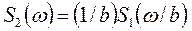)2.33-4)

Пример: Найти СПА гармонического сигнала u(t) = cosω₀t

Подставляя в (2.31) u(t) и формулу Эйлера 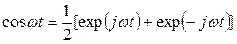, получим

.

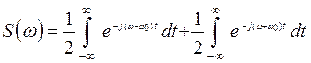На основании известного интеграла 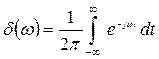получим СП

S(ω)=π[δ(ω-ω₀)+ δ(ω+ω₀)], (2.34))

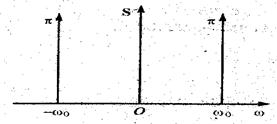Рис.2.12. СПА сигнала u(t) = cosω₀t.

СПА действительного гармонического сигнала расположена на частотах ±ω₀, симметричных относительно 0.

Наряду со спектральным анализом важен корреляционный анализ скорости изменения сигналов во временной области.

Корреляционный анализ. Для детерминированного финитного по t сигнала автокорреляционная функция (АКФ) равна (рис.2.13):

(2.35)

где B(0)=E²∙τ [дж, на R=1Oм], B(τ) = B(-τ)

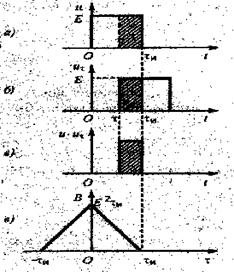Рис.2.13. АКФ финитного по t сигнала.

Для периодического детерминированного сигнала

.

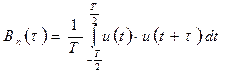Взаимная корреляционная функция (ВКФ) двух сигналов равна

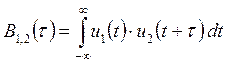(2.36)

АКФ для непериодического детерминированного и случайного сигнала определена энергетическим спектром (спектральной плотностью мощности (СПМ)) сигнала G(ω) [В²·С/Гц], через обратное преобразование Фурье

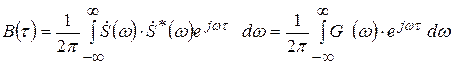, (2.37)

где прямое преобразование Фурье (СПМ) равно

. (2.38)

Для случайного стационарного процесса х(t) СПМ G_х(ω) определена прямым преобразованием Винера-Хинчина

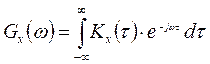, (Вт/Гц) (2.39)

где 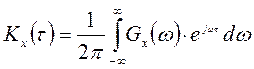, (2.40)

K_x(0) – средняя мощность процесса.

Дата добавления: 2014-01-13