Спектральный и корреляционный анализ

Колебание u(t) (сообщение, сигнал, помеху) с ограниченной энергией 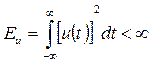можно аппроксимировать при помощи взвешенной линейной комбинации базисных функций :

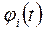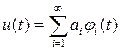(2.20)

где 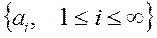- коэффициенты в аппроксимации u(t). Эти коэффициенты определяются из условия min ошибки аппроксимации, как

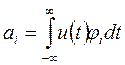и 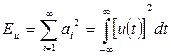(2.21)

При этом необходимо выполнение условия ортогональности

, при i ¹ j. (2.22)

и ортонормированности базисных функций

(2.23)

Разложение 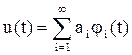называется обобщенным рядом Фурье.

Рассмотренный для сообщений ряд Котельникова и другие, например, известное представление нестационарного речевого сигнала ограниченными по времени и спектру вейвлетами являются частным случаем обобщенного ряда Фурье. Для эффективного сжатия сообщения необходим минимум членов ряда (2.20).

Если u(t) не равно 0 на интервале 0≤ t≤ Т, то это колебание может быть аппроксимировано тригонометрическим рядом Фурье

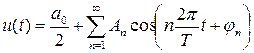, (2.24)

где коэффициенты амплитуд и фаз в аппроксимации равны:

;

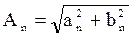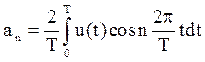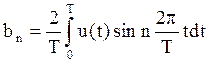; (2.25)

Для четной u(t)→b_n=0.

Амплитудный и фазовый спектры при таком представлении расположены в области положительных частот рис.2.4а,б, в частности, например, для периодических видеоимпульсов рис. 2.10г фазы φ_n гармоник принимают значения φ_n =± m π, где m=0,1,2,.., и при нечетных m амплитуды меняют знак, но модуль А _n. положителен для всех n.

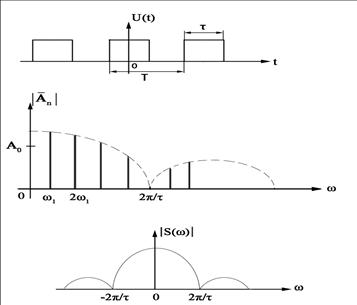г)

Рис. 2.10. Спектры тригонометрического и комплексного рядов Фурье.

.

Если колебание u(t) имеет ограниченную полосу частот до F_В, то количество спектральных составляющих (бесконечных по времени гармоник) будет, как и для ряда Котельникова, равно

(2.26)

и определяет число степеней свободы сигнала (базу сигнала).

Для комплексного ряда Фурье

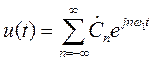(2.27)

комплексный амплитудный спектр

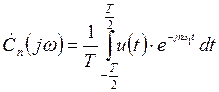(2.28)

расположен в обеих областях частот, например, для периодических сигналов 2.10в, а для непериодического видеоимпульса рис.2.4г в виде модуля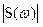спектральной плотности амплитуд (СПА) вида sin(х/х), который является огибающей амплитуд А _n для периодических видеоимпульсов.

т

Дата добавления: 2014-01-13