Условия эквивалентности

Теорема 5 позволяет установить простой критерий эквивалентности плоских систем сил. Прежде чем сформулировать его дадим два следующх определения.

Определение 3. Главным вектором R системы сил называют сумму всех её сил

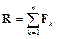
Определение 4. Главным моментом системы сил относительно точки О называют сумму моментов всех её сил относительно этой точки

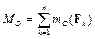
Теорема 6. Две системы сил эквивалентны тогда и только тогда, если равны их главные векторы и главные моменты относительно какой-нибудь одной и той же точки тела.

Доказательство. Равенство главных векторов и главных моментов означает, что после приведения (см.п.п.2.4) каждой из систем к одной и той же точке тела получаем равные силы и пары с равными моментами. Это и означает эквивалентность систем.

Обратно, для эквивалентных систем должны выполняться равенства главных векторов и главных моментов относительно произвольной точки О. В противном случае после приведения к этой точке каждой из систем получаем разные силы или (и) пары с разными моментами, т.е. неэквивалентные системы сил.

Задания для самостоятельной работы.

1. Докажите, что момент силы не изменится при переносе силы вдоль линии её действия.

2. Докажите, что система сил, состоящая из одной пары и одной силы, расположенной в плоскости этой пары, имеет равнодействующую.

3. Докажите, что произвольная плоская система сил либо эквивалентна одной силе, либо эквивалентна одной паре, либо уравновешена.

4. Докажите что для уравновешенности плоской системы сил необходимо и достаточно выполнение следующих условий

, , ,

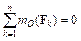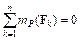где прямая АР, соединяющая моментные точки А и Р, не перпендикулярна оси х.

Дата добавления: 2014-01-13