Тема 5. Елементи векторної алгебри

План.

1. Вектори та дії над ними.

2. Проекція вектора на вісь.

3. Лінійно залежні і лінійно незалежні системи векторів.

4. Базис. Розклад вектора по базису. Система координат.

1. Вектором називається напрямлений відрізок. Позначаємо тощо. Основними характеристиками вектора є напрям та довжина (абсолютна величина). Довжина вектора позначається т.д. Вектор з нульовою довжиною називається нуль-вектором і позначається .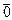

Означення 1: Колінеарними векторами називаються вектори, які розміщенні на одній прямій або на паралельних прямих.

Означення 2: Компланарні вектори, це вектори, які розміщуються в одній площині чи паралельних площинах.

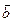Ветори та називаються рівними, якщо вони колінеарні, мають однакову довжину і напрямлені в один бік.

Операції над векторами.

1. Додавання векторів. Сумою двох векторів називається вектор, початок якого збігається з початком вектора- першого доданку, а кінець з кінцем вектора- другого доданку.

2. Різниця векторів. Різницею двох векторів та 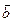називається вектор , такий, що .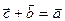

3. Добуток вектора на число. Добутком вектора на число a називається вектор, який має довжину |a | і який колінеарний вектору . Якщо a>0, то вектори a і однаково напрямлені, якщо a<0, то вектори a і мають протилежний напрямок.

Справедливе наступне твердження: Для того, щоб два вектори та 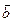були колінеарними наобхідно і досить, щоб їх можна було записати a= 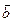, де a – дійсне число.

2. Як відомо проекцією точки А на пряму (площину) служить основа А₁ перпендикуляра АА₁, опущеного з цієї точки на пряму (площину). Нехай АВ - довільний вектор, а А₁, В₁- проекції його початку і кінця на вісь l. (Для побудови проекції точки А на пряму проводимо через точку А площину, перпендикулярну до прямої, перетин прямої і площини і визначає шукану проекцію). Нехай точки А та В мають координати А(х₁) та В(х₂). Проекцією вектора 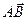на вісь l називається різниця координат (х₂ – х₁).

Теорема 1. Проекція вектора на вісь дорівнює добутку довжини вектора на косинус кута між вектором і віссю. Пр

Доведення:

З малюнка видно, що CD- проекція

вектора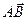на вісь l - дорівнює абсолютній

величині відрізка АК, а з трикутника АВК

випливає, що АК=АBcosРBAK. Теорему доведено.

Теорема 2. Проекція на вісь l суми двох векторів та 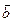дорівнює сумі проекцій на вісь l цих векторів.

Доведення теореми повністю

випливає з малюнка.

Теорема 3. Якщо вектор помножити на число a, то довжина його проекції також зміниться на величину, помножену на число a.

3. Вектори називаються лінійно залежними, якщо існують такі числа a₁, a₂,..., a_n, не всі рівні нулю, такі, що для них виконується рівність

. (1)

Вектори називаються лінійно незалежними, коли рівність (1) виконується тільки тоді, коли всі a₁, a₂,..., a_n дорівнюють нулю.

Нехай лінійно залежні і a₁№0. З рівності (1) випливає

, де .

Звідси видно, що у випадку лінійної залежності хоч один вектор є лінійною комбінацією всіх інших векторів.

Зрозуміло, що якщо вектори колінеарні, то вони лінійно залежні.

Теорема 1. Три вектори на площині – лінійно залежні.

Доведення:

Розглянемо наступні випадки:

1) серед векторів є колінеарні || 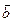. Тоді . З рівності бачимо, що не всі коефіцієнти рівні нулеві, але лінійна комбінація рівна нулю, тобто вектори лінійно залежні.

2) серед векторі в немає колінеарних. Тоді їх можна відкласти від одної точки.

Очевидно, що 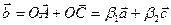. Таким чином, вектори лінійно залежні.

Теорема 2. Для того, щоб два вектори на площині були лінійно незалежні, необхідно і досить, щоб вони були неколінеарні.

Максимальне число лінійно незалежних векторів на площині рівне 2.

Аналогічно доводимо наступне:

1) Будь-які чотири вектори в просторі лінійно залежні.

2) Для того, щоб три вектори в просторі були лінійно незалежні, необхідно і досить, щоб вони були некомпланарні.

Максимальне число лінійно незалежних векторів в просторі рівне 3.

4. Базисом на площині називаються будь- які два лінійно незалежні вектори, взяті в певному порядку.

Позначимо два неколінеарні вектори, що утворюють базис, е₁, е₂.

Справедливе наступне твердження: Довільний вектор площини можна розкласти по векторах базису.

(Приймемо без доведення).

Аналогічно базисом в просторі називається будь-які три лінійно незалежні вектори, взяті в певному порядку (іншими словами три некомпланарні вектори утворюють базис).

Справедливе наступне твердження: Довільний вектор простору можна розкласти по векторах базису.

Впорядкована система трьох векторів, що визначають осі, разом з спільним початком і спільною одиницею довжини називається системою координат..

Впорядкована система трьох взаємно перпендикулярних векторів, що визначають осі, разом з спільним початком і спільною одиницею довжини називається прямокутною декартовою системою координат.

В цій впорядкованій системі, що позначається Oxzy, вісь Ox називається віссю абсцис, вісь Oy називається віссю ординат, вісь Oz називається віссю аплікат. Вектор, розкладений по векторах базису, спроектуємо на кожну з осей, і отримаємо відповідні проекції. Довжину проекції на осі абсцис назвемо абсцисою точки, початок якої лежить в початку координат, а кінець на кінці вектора. Аналогічно позначаємо ординату і аплікату точки.

Теорема. Будь- який вектор можна розкласти по ортам координатних осей.

Доведення випливає з теореми про розклад довільного вектора по трьох некомпланарних векторах і зауваження про те, що орти є некомпланарними векторами.

Розклад вектора по трьох ортах представимо у вигляді: . Коефіцієнтами цього розкладу служать проекції вектора на координатні осі, їх прийнято називати координатами вектора. Таким чином, коефіцієнтами розкладу вектора по осях служать його координати.

Робимо висновок про те, що довільному вектору простору можна поставити у відповідність трійку чисел (x,y,z), яка визначає його однозначно.

Внаслідок взаємної перпендикулярності координатних осей, довжина вектора , початок якого лежить в початку координат, рівна довжині діагоналі прямокутного паралелепіпеда, побудованого на векторах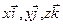і виражається рівністю .

Вектор можна виразити через координати початку і кінця. Нехай початок знаходиться в точці , а кінець - в точці . Тоді з рівності маємо

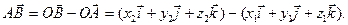
Звідси , або

Операції над векторами, заданими координатами:

1. Сумою двох векторів та є вектор

2. Різницею двох векторів та є вектор 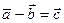де

3. Добутком вектора на число a є вектор a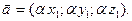

Аналогічні операції можна проводити над векторами на площині.

Дата добавления: 2014-01-13