
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція 2.2. Скалярний, векторний та мішаний добуток векторів
|
|
|
|
Контрольні запитання
1. Що називається вектором? Які його основні характеристики?
2. Які вектори називаються колінеарними, компланарними?
3. Сформулюйте і доведіть ознаку колінеарності векторів.
4. Що називається сумою, різницею векторів, добутком вектора на число?
5. Що називається проекцією вектора на вісь?
6. Сформулюйте і доведіть основні властивості проекцій.
7. Які вектори називаються лінійно залежними, лінійно незалежними? Які їх основні властивості?
8. Що таке базис? Сформулюйте і доведіть основну властивість базису.
9. Що таке система координат, координата точки, координати вектора?
Сформулюйте правила для дій над векторами, заданими координатами.
План.
1. Скалярний добуток векторів та його застосування.
2. Векторний добуток векторів та його застосування.
3. Мішаний добуток трьох векторів.
1. Розглянемо два вектори, для спрощення взявши їх в тривимірній системі координат. Нехай дано вектори 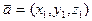 та
та 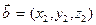 .
.
Означення. Скалярним добутком двох векторів називається число рівне добутку довжин цих векторів на косинус кута між ними. 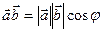 .
.
Виразимо скалярний добуток в координатній формі. Спочатку знайдемо скалярний добуток ортів. За означенням
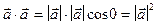 .
.
Тобто скалярний добуток вектора самого на себе дорівнює квадрату довжини вектора. Зокрема  . З попарної перпендикулярності векторів-ортів системи координат слідує:
. З попарної перпендикулярності векторів-ортів системи координат слідує:  .
.
Перемножимо два вектори:
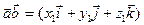
 =
=
= =
=
=(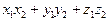 ).
).
Справедлива теорема. Скалярний добуток двох векторів дорівнює сумі добутків однойменних координат цих векторів.
Доведення наведено вище.
Властивості скалярного добутку векторів:
1. Властивість переміщення.  .
.
Доведення.
Так як кут між векторами  та
та 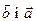 один і той самий, і добуток їх абсолютних величин є добутком чисел, тобто задовільняється переставний закон для добутку абсолютних величин, то, за означенням, властивість справджується.
один і той самий, і добуток їх абсолютних величин є добутком чисел, тобто задовільняється переставний закон для добутку абсолютних величин, то, за означенням, властивість справджується.
2. Властивість об’єднаності по відношенню до множення вектора на число.
(Довести самостійно).
3. Розподільна властивість скалярного множення відносно додавання векторів.
Доведення.
Використаємо очевидний наслідок, про те, що 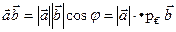 . Тоді, якщо
. Тоді, якщо 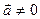 , то
, то 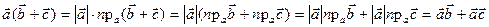 .
.
Якщо ж  , то рівність очевидна.
, то рівність очевидна.
Знайдемо кут між векторами, заданими своїми координатами.
За означенням 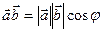 . Звідси
. Звідси 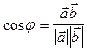 .
.
Тобто, косинус кута між ненульовими векторами дорівнює скалярному добуткові цих векторів, поділеному на добуток їх абсолютних величин.
Якщо вектори задані координатами 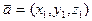 та
та 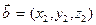 , то
, то 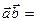
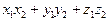 , і
, і  і
і  .
.
Таким чином, 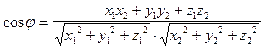 .
.
З останньої формули випливає, що для того, щоб вектори були перпендикулярними, необхідно і досить, щоб їх скалярний добуток був рівний нулеві.
2. Означення. Векторним добутком векторів 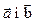 називається вектор
називається вектор 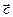 , який визначається наступними умовами:
, який визначається наступними умовами:
1) модуль вектора 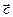 дорівнює
дорівнює  , де j- кут між векторами
, де j- кут між векторами 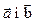 ,
,
2) вектор 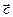 перпендикулярний до площини, що визначається векторами
перпендикулярний до площини, що визначається векторами 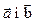 ,
,
3) вектор 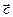 напрямлений так, що спостерігачеві, який дивиться з його кінця на вектори
напрямлений так, що спостерігачеві, який дивиться з його кінця на вектори 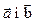 , здається, що для найшвидшого суміщення першого вектора з другим, перший вектор потрібно переміщати проти годинникової стрілки.
, здається, що для найшвидшого суміщення першого вектора з другим, перший вектор потрібно переміщати проти годинникової стрілки.
Векторний добуток позначаємо символом  .
.
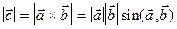 .
.
Властивості векторного добутку.
1. Векторний добуток рівний нулеві, якщо перемножувані вектори колінеарні, або хоч один з них є нульовим.
2. При перестановці місцями векторів співмножників, векторний добуток міняє знак на протилежний 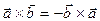
Тобто векторний добуток не має властивості перестановки.
3. Виконується розподільна властивість: 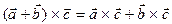
Знайдемо вираз векторного добутку через прямокутні декартові координати векторів. Нехай дано два вектори 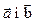 . Причому
. Причому 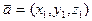 та
та 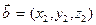 , задані своїми координатами в прямокутній декартовій системі координат.
, задані своїми координатами в прямокутній декартовій системі координат.
Розкладемо вектори за базисними:
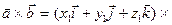
 =
=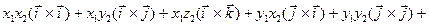
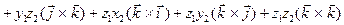
За означенням: 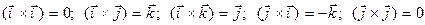 ;
; 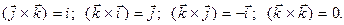
Тому 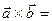
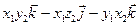
 , або
, або
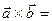
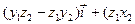
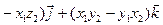 .
.
Отримана формула досить громіздка, тому для запам’ятовування використовують іншу, виражену через визначник.

а потім, обраховують його за розкладом по елементах першого рядка.
Означення. Мішаним добутком трьох векторів 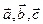 називається число, рівне скалярному добутку векторного добутку
називається число, рівне скалярному добутку векторного добутку 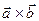 на вектор
на вектор 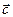 . Позначаємо
. Позначаємо  .
.
З геометричної точки зору мішаний добуток рівний об’єму паралелепіпеда, побудованого на векторах 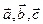 .
.
Справедливі наступні твердження:
1. Мішаний добуток трьох векторів рівний нулю тоді і тільки тоді, коли вектори 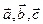 компланарні.
компланарні.
2. Для довільних векторів 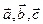 справедливі рівності:
справедливі рівності:  =
=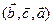 =
=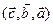 .
.
Можна довести наступне: Мішаний добуток трьох векторів визначається за формулою: 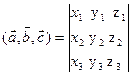 .
.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 6267; Нарушение авторских прав?; Мы поможем в написании вашей работы!