Метод парабол (квадратической апроксимации)

Апроксимация – это замена неизвестной функции известной функцией в окрестности какой-то точки. Алгоритм метода: 1) Задается начальная точка x0 (недалеко от точки минимума или максимума);

2) Вычисляются две точки: x ₁ = x ₀ – e и x ₃ = x ₀ + e, где e – точность расчетов);

3) Вычисляются значения функции в этих точках f ₀ = f(x ₀), f ₁ = f(x ₁) и f ₂ = f(x ₂);

4) По этим значениям строится парабола p(x)=ax ² + bx + c.

5) Находится вершина параболы: .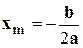

6) Если выполняется условие ½ x ₀ – x _m½ < e, то расчеты прекращаются и точкой минимума считается точка x* = x _m. В противном случае x ₀ = x _m и все повторяется с пункта 2.

Коэффициенты a, b, c можно получить, решив следующую систему линейных уравнений:

или A×X = B, где

Недостатки этого метода:

– заранее нельзя сказать, что будет найдено – минимум или максимум. Только после процесса оптимизации можно определить что нашли (min или max) по коэффициенту a: при a < 0 – нашли max. При a > 0 – нашли min;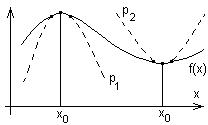
– этот метод нельзя применить при наличии ограничений. Он не позволяет найти экстремумы на границах отрезка;

– метод вообще не применим в случае линейных функций. Если исходная функция f(x) линейна, то в параболе коэффициент a = 0, т.е. нельзя найти

.

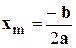Достоинства:

– один из самых быстродействующих методов;

– не требует определения начального отрезка (нужна только начальная точка);

– для квадратичной функции этот метод находит точное решение за один шаг (это самое основное достоинство).

Пример: f(x) = x ² + 4 x + 2

1) x ₀ = 1, e = 1.

2) x ₁ = 0, x ₂ = 2.

3) f ₀ = 7, f ₁ = 2, f ₂ = 14.

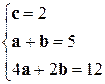4) Þ 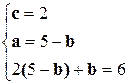Þ Þ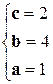

5) .

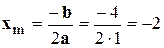Коэффициенты a, b, c совпали с коэффициентами исходной функции.

Метод парабол в основном применяется в безусловной оптимизации квадратических функций.

Дата добавления: 2014-01-13