Метод золотого сечения

При решении оптимизационных задач очень важен выбор двух пробных точек, позволяющих сузить интервал поиска. Для построения наиболее рациональной стратегии поиска оптимального решения эти точки должны удовлетворять следующим условиям: пробные точки следует размещать симметрично относительно середины интервала (как и в методе дихотомии); пробные точки должны размещаться таким образом, чтобы отношение длины исключаемого подинтервала к длине интервала поиска оставалось постоянным, т.е. две точки располагаются таким образом, чтобы на следующем этапе одна из них оказалась в нужном месте.

Точка x2 оказывается в том же месте в новом отрезке, что и точка x1 в старом отрезке или точка x1 оказывается в том же месте, что и точка x2. Выполнение этих условий обеспечивает необходимость вычисления на каждом шаге только одного значения функции.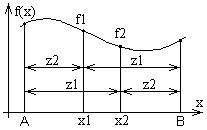

Кроме того, мы получим сочетание требований, при которых удаляемый интервал будет возможно наибольшей длины и число шагов будет минимальным.

Определим длину нового интервала z ₁:

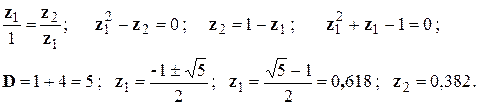
Т.к. новый отрезок составляет 0,618 от исходного, то . Число 1,618 называется золотым сечением. Алгоритм выбора нового отрезка такой же, как и в методе дихотомии.

Достоинства: самый быстродействующий из общих методов.

Недостатки: такие же, как у метода деления отрезка пополам.

Дата добавления: 2014-01-13