Метод прямого поиска

Его еще называют методом прямого перебора вариантов.

Алгоритм метода:

Исходный интервал неопределенности [A0, B0]делится на N отрезков, на границах которых вычисляются значения функции и сравниваются друг с другом. Среди этих значений выбирается минимальное (или максимальное).

; N= 2 K_C;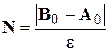

Преимущества метода прямого поиска заключаются:

1) в независимости поиска от вида и характера целевой функции;

2) в цикличности поисковой процедуры;

3) в определении глобального экстремума целевой функции;

4) в простоте алгоритма и программы оптимизации;

5) в малом объеме необходимой машинной памяти.

Главным недостатком метода является продолжительное время работы ЭВМ.

Это единственный метод оптимизации, который позволяет найти глобальный минимум или максимум. Но этот метод неприменим для многомерных функций из-за очень большого количества вычислений целевой функции. Если n – количество переменных, то количество вычислений целевой функции N = (2KC)^n.

Далее, рассмотрим три метода одномерного поиска, ориентированных на нахождение точки оптимума внутри заданного интервала путем последовательного уменьшения интервала поиска. Эти методы носят название методов исключения интервалов. Все они основаны на очень важном свойстве функции – унимодальности. Во всех этих методах предполагается, что на исследуемом интервале функция унимодальна и сравнение значений f(X) в нескольких точках интервала позволяет определить, в каком из подинтервалов, заданных этими точками, точка оптимума отсутствует (или находится).

Достоинством этих методов является исключение необходимости полного перебора всех допустимых точек (как в предыдущем методе). Так как они могут быть основаны только на вычислении значений функции, то исследуемая функция может быть и недифференцируемой.

Дата добавления: 2014-01-13