
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Непрерывность сложной ф-ии
|
|
|
|
Пусть:
1. Ф-ия  - непрерывна в т. y0.
2. Ф-ия - непрерывна в т. y0.
2. Ф-ия 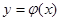 - непрерывна в т. х0.
3. - непрерывна в т. х0.
3. 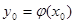
|
Þтогда сложная ф-ия 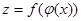 - непрерывна в т. х0. - непрерывна в т. х0.
|
Доказательство:
А). 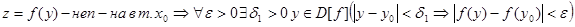
Б).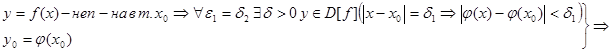
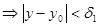
из А) и Б) следует:

Sl. 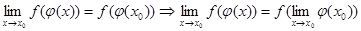
Непрерывность ф-ии на множестве.
Df. Ф-ия непрерывна на множестве Х, если она непрервна в каждой точке этого меожества.
Непрерывность обратной ф-ии:
Пусть 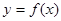 - непрерывна и строго монотонна на промежуте Х, тогда справедливо:
- непрерывна и строго монотонна на промежуте Х, тогда справедливо:
1. *****
2. На промежутке Y существует непрерыная обратная ф-ия 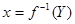 .
.
3. Характер монотонности обратной ф-ии такой же как и прямой.
Непрерывность элементарной ф-ии:
1. **********
2. Доказательство непрерывности основной элементарной ф-ии tg и ctg, следует из свойств непрерыности элементарных ф-ий.
3. Непрерывность log, arcsin, arccos, arstg следует из определения непрерывности обратной ф-ии.
Df Элементарные ф-ии, полученные из основных элементарных ф-ий с помощью арифметических операций, взятых в конечном числе,********
Характеристика точек разрыва ф-ии.
1. Точка устранимого разрыва.
D(f) т. х0 называется точкой устранимого разрыва ф-ии 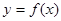 , если она не определена в этой точке, но имеет конечный предел.
, если она не определена в этой точке, но имеет конечный предел.
Ф-ию можно сделать непрерывной в этой точке, доопределив ей значение в этой точке равным пределом.

2. Точка разрыва первого рода.
D(f) х0 – точка разрыва первого рода, если существует конечный левосторонний и правосторонний предел не равные между собой.
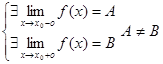
Разницу (b-a)называют скачком ф-ии в т. х0
3. Точка разрыва второго рода.
*********************************
Односторонняя непрерывность ф-ии.
1. Если в D(f) 1 непрерывности предел заменить односторонним пределом, то получим определение односторонней непрерывности ф-ии.
2. Ф-ия называется непрерывной в точке х0 справа, если правосторонний предел совпадает со значением ф-ии.
3. Ф-ия называется непрерывной в точке х0 слева, есди левосторонний предел совпадает со значением ф-ии.
Например:
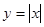 - исследуем предел ф-ии справа и слева:
- исследуем предел ф-ии справа и слева:
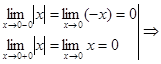 ф-ия непрепывна в точке х=0.
ф-ия непрепывна в точке х=0.
Для непрерывности в точке х0 необходимо и достаточно, чтобы она была непрерывна слева и справа в этой точке.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 474; Нарушение авторских прав?; Мы поможем в написании вашей работы!