Лекція 3.2. Пряма лінія на площині

План.

1. Різні види рівняння прямої на площині.

2. Загальне рівняння прямої.

3. Деякі застосування рівняння прямої на площині.

1. Положення прямої на площині можна задати наступним чином:

1) пряма l проходить через точку M₀, паралельно до вектора ; точку M ₀ в цьому випадку ще називають заданою точкою;

2) пряма l проходить через точку M₁ і М₂;

3) пряма l проходить через точку M ₀, перпендикулярно до вектора ;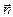

4) пряма l проходить через точку M ₀, утворюючи з вектором деякий кут j.

Довільний вектор №0, що паралельний прямій l, називається напрямним вектором цієї прямої. З цього означення слідує, що кожна пряма має як завгодно багато напрямних векторів і всі вони колінеарні між собою.

Довільний вектор 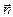№0, перепендикулярний до прямої l, називається нормальним вектором цієї прямої. З цього означення слідує, що кожна пряма має як завгодно багато нормальних векторів і всі вони колінеарні між собою.

Якщо на прямій l взяти дві довільні точки M₁ і М₂, то вектор 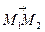є напрямним вектором для прямої, так само і вектор 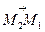є напрямним, бо він колінеарний вектору 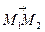і, взагалі, довільний вектор k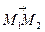буде напрямним вектором для прямої l.

Розглянемо всі випадки задання прямої на площині:

1. Нехай пряма l задана початковою точкою M ₀ і напрямним вектором . Нехай М - довільна точка, її радіус-вектор позначимо через 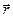. Вектор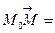 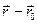паралельний прямій тоді і тільки тоді, коли точка М належить цій прямій. У цьому випадку вектор 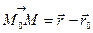колінеарний вектору . Тобто, існує таке число t, що

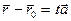. (1)

Змінна t, задана в формулі називається параметром, а рівняння (1) - векторно - параметричним рівнянням прямої l.

Якщо координати точок позначити через М(x; y), M₀(x₀; y₀), а координати вектора 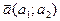, то рівняння (1) перепишеться у вигляді

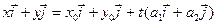
або

.

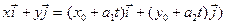Звідси

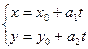. (2)

Рівняння (2) називаються параметричними рівняннями прямої.

Виключимо параметр t з рівняння. Це можливо, оскільки напрямний вектор не нульовий, отже, хоч одна з його кординат не рівна нулеві.

Припустимо, що 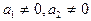. Тоді

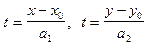
і, значить,

. (3)

Рівняння (3) називають канонічним рівнянням прямої з напрямним вектором .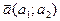

Якщо 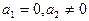, то рівняння прийме вигляд

.

Очевидно, що така пряма паралельна до осі Oy, а її канонічне рівняння матиме вигляд x=x₀.

Якщо 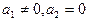, то рівняння прийме вигляд

.

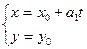Очевидно, що така пряма паралельна до осі Oх, а її канонічне рівняння матиме вигляд y=y₀.

2. Нехай дані дві точки М₁ і М₂, задані своїми координатами (x₁; y₁), (x₂; y₂). Щоб скласти рівняння прямої, що проходить через точки М₁ і М₂, будемо вважати вектор 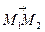= напрямним вектором прямої. Тоді канонічне рівняння прямої з попереднього пункту, враховуючи, що координати вектора М₁М₂= будуть мати координати 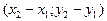, перпишеться у вигляді

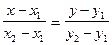(4)

Це рівняння називається рівнянням прямої, що проходить через дві задані точки.

Якщо в рівнянні (4) один з знаменників перетворюється в нуль, то для написання рівняння варто прирівняти до нуля відповідний чисельник. Наприклад, якщо 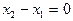, то шуканим рівнянням буде рівняння x=x₁. В цьому випадку точки знаходяться на однаковій відстанні від осі Oy і пряма буде паралельна цій осі.

Часто потрібно написати рівняння прямої, що проходить через точки, що лежать на координатних осях. Нехай це будуть точки A(a; 0) i B(0; b). Вважаючи в формулі (4), що x₁=a, y₁=0, x₂=0, y₂=b, маємо

або .

Це рівняння називається рівнянням прямої у відрізках, так як числа a i b показують, які відрізки відсікає пряма від осей.

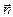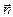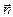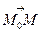3. Нехай дана деяка точка М₀ і вектор . Проведемо через точку М₀ пряму l, перпендикулярно до вектора . Нехай М - довільна точка. Тоді М лежить на прямій l тоді і тільки тоді, коли вектори і перпендикулярні між собою, а для перепендикулярності векторів досить, щоб їх скалярний добуток дорівнював нулю.

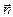
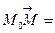0. (5)

Нехай М(x; y), М₀ (x₀; y₀). Тоді вектор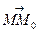 (x-x₀ ; y- y₀). Позначимо координати нормального вектора (A; B). Тоді (5) перепишеться у вигляді

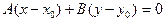. (6)

Рівняння (6) - рівняння прямої l, що проходить через точку М₀(х₀; y₀), перпендикулярно до вектора 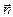(A; B).

4. Нехай на площині, де є прямокутна система координат, пряма l проходить через точку М₀ паралельно напрямному вектору . Якщо пряма перетинає вісь Ox в точці N, то під кутом між прямою і віссю будемо розуміти кут між прямою і віссю, менший 180⁰. Цей кут називають кутом нахилу прямої до осі. Якщо пряма паралельна осі Ox, то кутом між ними приймаємо кут рівний нулю.

Тангенс кута нахилу прямої до осі називається кутовим коефіцієнтом прямої і позначається буквою k. Кутовий коефіцієнт прямої можна обчислити, якщо відомі координати довільних двох точок, що належать прямій.

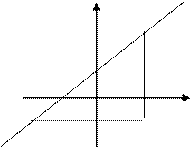
З прямокутного трикутника М₁РМ₂ (див. мал.1) маємо

М₂ ;

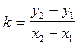. (7)

Р

М₁

Мал.1

Формула (7) не має смислу, якщо х₂=х₁, тоді пряма паралельна осі Oy і кутовий коевіцієнт не існує.

Складемо рівняння прямої, заданої кутовим коефіцієнтом та деякою точкою. За початкову точку візьмемо М₀(x₀;y₀), а за довільну М(x;y). Тоді (7) перепишеться як

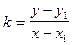. (8)

Якщо ж точка М не належить прямій l, то (8) не виконується. Це рівняння записують, як правило, у вигляді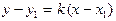

Якщо пряма перетинає вісь Oy в деякій точці (0: b), то рівняння набуде вигляду y=kx+b.

Це рівняння називають рівнянням прямої з кутовим коефіцієнтом k і початковою ординатою b.

2. Нехай дано довільну пряму. Виберемо на ній деяку точку М₀(x₀;y₀) і нормальний вектор 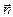(A; B). Тоді рівнянням прямої буде вираз

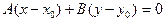
Перепишемо його у вигляді .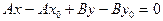

Позначивши через С, отримаємо

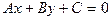(1)

Таким чином, довільна пряма площини визначається рівнянням (1), тобто лінійним рівнянням з двома невідомими.

Покажемо тепер, що довільне лінійне рівняння обов’язково визначає деяку пряму. Дійсно, в рівнянні (1) принаймі один з коефіцієнтів відмінний від нуля. Припустимо, що це коефіцієнт В. Тоді (1) перепишеться як

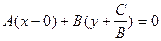. (2)

З пункту 3 попереднього питання маємо, що (2), а значить і (1) визначає пряму, що проходить через точку (0; -C/B) і перпендикулярну вектору 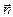(A; B).

Рівняння 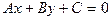називають загальним рівнянням прямої. Якщо А=0, то рівняння набуде виду y=-C / B. Тобто всі точки мають одну ординату і пряма паралельна осі Ox.

Якщо А=0, С=0, то y=0, - пряма є рівнянням осі Ox. Аналогічно (покажіть це самостійно), якщо В=0, то пряма паралельна осі Oy.

Якщо В=0, С=0, то пряма є віссю Oy.

3. Нехай маємо дві прямі

l ₁: A₁x+B₁y+C₁=0;

l₂: A₂x+B₂y+C₂=0.

Позначимо через j - кут між цими прямими. Зрозуміло, що цей кут рівний кутові між нормальними векторами двох заданих прямих.

За формулою кута між двома векторами маємо:

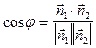(1)

Переписавши формулу (1) через координати отримаєм:

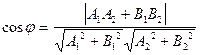
Це формула обрахування кута між двома прямими, заданими напрямними векторами.

Звідси: прямі паралельні тоді і тільки тоді, коли вектори колінеарні, тобто

.

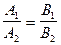Прямі перпендикулярні тоді і тільки тоді, коли скалярний добуток векторів рівний нулю, тобто

.

Якщо дві прямі задані рівняннями з кутовими коефіцієнтами y=k₁x+b₁; y=k₂x+b₂, то

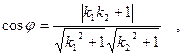
або .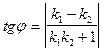

Якщо дві прямі задані через фіксовану точку та напрямний вектор, то косинус кута між ними визначається через координати напрямних векторів наступним чином.

.

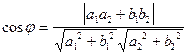Відстань від точки до прямої дорівнює модулю числа, отриманого в результаті підстановки координат точки в рівняння прямої виду

0.

Тут вираз називають нормованим множником.

Дата добавления: 2014-01-13