Канонічне рівняння гіперболи

(Проведіть доведення самостійно).

Дослідимо форму гіперболи.

1) гіпербола має дві осі симетрії і центр симетрії - точку початку координат.

2) При y=0 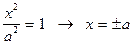тобто точки 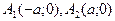належать гіперболі. При х=0 - 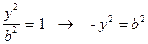® рівняння розв’язку не має.

Вісь симетрії, яка перетинає гіперболу називається дійсною віссю (це вісь Ох). 2а=А₁А₂ – називається дійсною віссю гіперболи, а – дійсна піввісь. Вісь симетрії, яка не перетинає гіперболу називається уявною віссю (це вісь Оy), 2b – уявна вісь, b – уявна піввісь.

3) Розглянемо 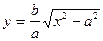. Звідси видно, що при зростанні х зростає y.

4) Розглянемо пряму 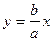і деяку точку N(x; y), що належить гіперболі. Знайдемо відстань від прямої до точки. Обчислимо відстань від точки М, що лежить на прямій до точки N, коли вони мають однакові абсциси.

.

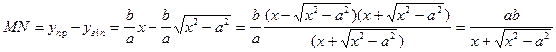Якщо х®Ґ, то MN®0. Але відстань між точкою і прямою менша за знайдену нами MN, тому MP®0 також. За означенням, пряма 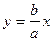- асимптота гіперболи. Враховуючи симетрію гіперболи маємо 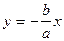- також асимптота гіперболи.

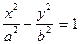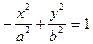Гіперболи виду і називаються спряженими.

Якщо a=b, то гіпербола називається рівнобічною.

Аналогічно до поняття ексцинтриситету еліпса, вводимо поняття ексцинтриситету гіперболи. 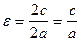, e>1. Велична e характеризує форму гіперболи.

e - називаємо ексцентриситетом гіперболи.

Директриса гіперболи – це пряма, яка проходить перпендикулярно до дійсної осі на відстанні 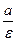від центра. Тобто, існує дві директриси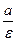: х =і х=-.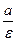

3. Парабола - геометричне місце точок, рівновіддалених від заданої точки (фокуса) та заданої прямої (директриси).

Нехай задано точку F і пряму p. Точка М(x, y) буде належати параболі, якщо MР=MF, де N - основа перпендикуляра опущеного з точки М на пряму. Нехай 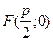, а рівняння директриси 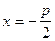. Тоді . Це рівняння є рівнянням параболи. Проведемо ряд перетворень:

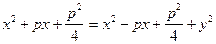
- канонічне рівняння параболи.

Дослідимо форму параболи:

1) парабола має вісь симетрії Ox.

2) при y=0 маємо x=0, тобто точка О(0; 0) належить параболі і її називають вершиною параболи.

3) Так як в лівій частині рівності завжди число не від’ємне, то 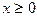, тобто крива розміщена в додатній півплощині відносно x.

4) 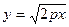. При зростанні x абсолютна величина y зростає.

Дата добавления: 2014-01-13