Видно, що ,( тобто площина паралельна до осі Ox

3. Якщо А=0; D=0 Ю By+Cz=0 – площина проходить через Ох;

4. При А=0; В=0 Ю Cz+D=0 площина паралельна до площини хОy.(C№0; z=-D/C).

5. А=0; В=0; D=0 Ю Cz=0; C№0 ® z=0 – координатна площина xOy.

2. Рівняння площини, яка проходить через дані три точки. Нехай задано три точки 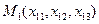, , 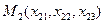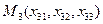. Виберемо довільну точку 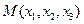. Тоді вектори 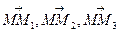- компланарні і їх мішаний добуток рівний нулеві.

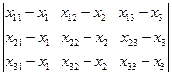=0. (3)

Остання рівність розписується за елементами першого рядка і зводиться до загального рівняння площини.

Рівняння площини у відрізках. Нехай площина перетинає координатні осі відповідно в точках P(a;0;0), Q(0;b;0), R(0;0;c)

Складаємо рівняння площини, використовуючи рівняння (3) і підставляючи координати точок Р, Q, R знайдем визначник.

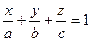(4)

Нормальне рівняння площини. Нехай відомо, що вектор p=OP, що відповідає деякій точці Р, яка належить заданій площині, утворює з координатними осями кути a, b, g відповідно. Без доведення запишемо рівняння такої площини.

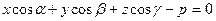. (5)

Таке рівняння називається рівнянням площини в нормальному вигляді. До загального воно зводиться так:

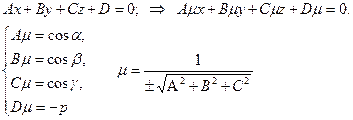
3. Так як пряма є лінією перетину двох площин, то загальне рівняння прямої в просторі можна задати у вигляді:

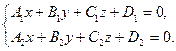(1)

Коефіцієнти A₁, B₁, C₁, A₂, B₂, C₂ не є пропорційними.

Розглянемо поняття пучка площин.

Нехай 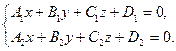- деяка пряма в просторі.

Пучком площин називається сукупність площин, які проходять через дану пряму. Пряма в такому випадку називається віссю пучка.

При довільному l рівняння виду

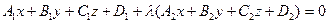(2)

визначає площину.

Доведемо, що рівняння (2) визначає пучок площин з віссю (1).

Очевидно, що при будь- якому l площина (2) проходить через пряму (1). Виберемо точку M₁ (x₁,y₁,z₁) і покажемо, що при деякому l з рівняння (2) можна отримати рівняння площини, що проходить через (1) і задану точку.

Якщо 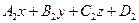¹0, то

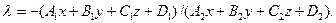
Отже, рівняння (2) при довільному l визначає пучок площин.

Приклад. Скласти рівняння пучка площин, який проходить через пряму

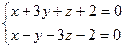і точку M(2;1;1).

Розв’язання.

x-3y+z+2+l(x-y-3z-2)=0,

2+3+1+2+l(2-1-3-2)=0,

8-4l=0,

l=2.

x-3y+z+2+2(x-y-3z-2)=0,

3x+y-5z-2=0.

4. Нехай задано точку М₁(х₁, y₁, z₁), що належить прямій і вектор 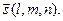напрямний до неї. Виберемо довільну точку М(x,y,z) цієї прямої. Аналогічно до рівняння прямої на площині маємо, що колінеарний вектору 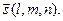За ознакою колінеарності

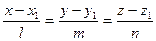
Ці рівняння називають канонічними рівняннями прямої. Взявши t – параметр колінеарності, маємо

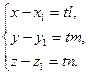
Отримали параметричне рівняння прямої з параметром t.

Нехай задано точки M ₁ (x₁, y₁, z₁) та М₂ (x₂, y₂, z₂), що належать площині тоді вектор 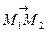напрямний до неї. Виберемо довільну точку М(x,y,z) цієї прямої. Використовуючи канонічне рівняння прямої маємо

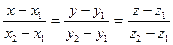
Для того, щоб звести загальне рівняння до канонічного виду потрібно:

1) Знайти координати деякої точки М, що належить прямій, враховуючи, що точка перетину прямої і координатної площини має одну координату рівну нулеві, а дві інші однозначно визначаються з загального рівняння.

2) Знайти напрямний вектор прямої, обчисливши його координати як координати векторного добутку двох векторів нормалей до площин, рівняння яких записанні в загальному рівнянні прямої.

3) Записати рівняння прямої через точку та напрямний вектор.

Дата добавления: 2014-01-13