Лекція 3.4-3.5. Площина та пряма в просторі

Контрольні запитання

1. Що називається еліпсом, його фокусами, осями, ексцентриситетом та директрисою?

2. Дослідіть форму еліпса і побудуйте його.

3. Що називається гіперболою, її фокусами, осями, ексцентриситетом та директрисою?

4. Дослідіть форму гіперболи і побудуйте її.

5. Вкажіть, які прямі є асимптотами гіперболи і доведіть це.

6. Що називається параболою, її фокусом та директрисою?

7. Дослідіть форму параболи і побудуйте її.

План.

1. Загальне рівняння площини.

2. Різні види рівняння площини:

а) рівняння площини, що проходить через три точки;

б) рівняння площини у відрізках;

в) нормальне рівняння площини.

3. Загальне рівняння прямої. Пучок площин.

4. Канонічне рівняння прямої. Рівняння прямої, що проходить через дві задані точки.

5. Деякі задачі для площини та прямої в просторі.

1. Розглянемо рівняння площини, що проходить через задану точку, перпендикулярно до деякого вектора. Нехай це точка M₀ (x_0і y₀, z₀) i вектор . Заданий вектор, як і у випадку з прямою на площині, назвемо нормальним. Якщо деяка точка М належить площині, то зрозуміло, що 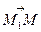перпендикулярний до , тобто їх скалярний добуток рівний нулю.

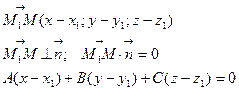. (1)

Тут А, В, С –координати вектора, перпендикулярного до площини.

Таке рівняння називається загальним рівнянням площини.

Теорема: Кожна площина визначається рівнянням І степеня відносно декартових координат x; y; z: Ах+Вy+Cz+D=0. Обернено: Кожне рівняння І степеня відносно x;y;z визначає в просторі площину:

Доведення.

Розпишемо загальне рівняння площини в наступному вигляді:

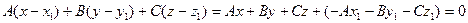
Вираз в дужках є дійсним числом, тобто його можна перепозначити через D, що доводить пряму теорему.

Навпаки, нехай відоме Ax+By+Cz+D=0 (2)

Нехай С№0, перепишемо вираз (2) у вигляді:

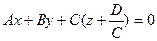
А це рівняння площини, що проходить через точку M₁(0;0;-D/C) і має нормальний вектор .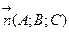

Розглянемо кілька окремих випадків.

1. Якщо D=0 Ю Ax+By+Cz=0 – площина проходить через О(0;0;0)

2. Якщо А=0 Ю By+Cz+D=0

Дата добавления: 2014-01-13