Аналогічно розглядаються випадки, коли напрямна лежить у інших координатних площинах

Поверхнею обертання називається поверхня, утворена внаслідок повороту деякої лінії навколо заданої осі.

Еліпсоїд – поверхня, яка в деякій вибраній системі координат має канонічне рівняння у вигляді:.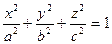

Дослідимо форму еліпсоїда методом паралельних перерізів.

Нехай .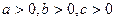

1) 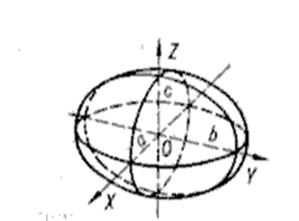При перерізі площиною xOy

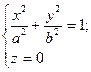, отже, в перерізі є еліпс.

Аналогічно

2) При перерізі площиною xOz 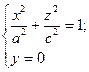– в перерізі - еліпс.

3) При перерізі площиною zOy 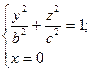– в перерізі - еліпс.

4) Розглянемо переріз, утворений в результаті перетину деякою некоординатною площиною. Наприклад, z=p.

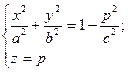
якщо 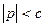, то отримаємо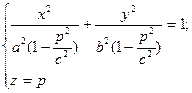

Це рівняння еліпса з півосями , .

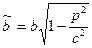При 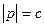отримаємо дві точки (0;0;с) i (0;0;-c).

При 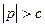, , площина еліпсоїда не перетинає.

Аналогічні результати можна отримати при розгляді перетину еліпсоїда площинами перпендикулярними іншим координатним осям. З виразів 1), 2), 3) випливає, що еліпсоїд має три площини симетрії, які співпадають з координатними площинами.

Якщо 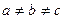, то еліпсоїд є триосним, якщо 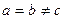, то отримуємо еліпсоїд обертання (еліпс 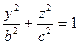обертається навколо осі Oz). При 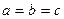отримаємо рівняння сфери.

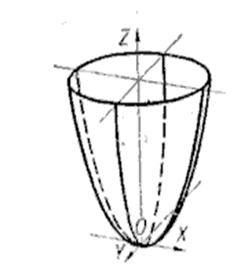
2. Еліптичний параболоїд - це поверхня, рівняння якої в деякій вибраній системі координат має вигляд: 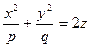, де p, q – числа одного знаку.

Проведемо дослідження його форми.

Нехай p>0, q>0, тоді і z³0. Фактично це означає, що дана поверхня лежить в додатньому півпросторі відностно площини xOy.

1) При перерізі площиною xOy

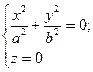, площина дотикається до поверхні в точці О(0;0;0).

2) При перерізі площиною xOz

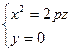– в перерізі - парабола.

3) При перерізі площиною zOy

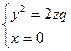– в перерізі – парабола.

4) Розглянемо переріз, утворений в результаті перетину деякою площиною. z=h..

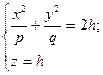
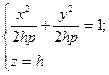. Зрозуміло, що h>0.

Це еліпс з півосями , .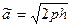

Еліптичний параболоїд має дві площини симетрії.

При p=h отримаємо 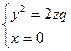– параболоїд обертання навколо осі Oz.

При p<0, q<0 отримаємо параболоїд, симетричний вищерозглянутому відносно xOy.

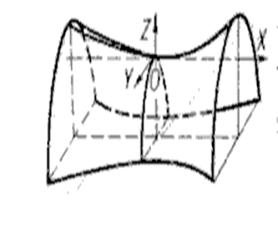
Гіперболічний параболоїд - це поверхня, рівняння якої в деякій вибраній системі координат має вигляд: 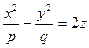, де p, q – числа одного знаку.

Проведемо дослідження його форми.

Нехай p>0, q>0. Так як x,y входять в рівняння в квадраті, то поверхня має дві площини симетрії xOz, yOz.

1) При перерізі площиною xOy 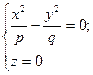, або 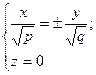– пара прямих, що проходить через О(0;0;0).

2) При перерізі площиною xOz 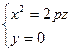– в перерізі - парабола.

3) При перерізі площиною zOy 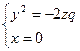– в перерізі – парабола.

4) Розглянемо переріз, утворений в результаті перетину деякою площиною. z=h..

–

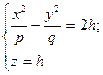
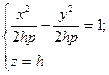гіпербола, якщо h<0, то дійсна вісь паралельна осі Oy, якщо h>0, то дійсна вісь паралельна Ox.

5) Розглянемо переріз, при x =h..

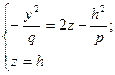
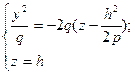– парабола.

3. Однопорожнинний гіперболоїд – це поверхня, рівняння якої в деякій вибраній системі координат має вигляд: .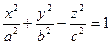

Проведемо дослідження аналогічне як для еліпсоїда.

1)При перерізі площиною xOy 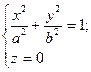, отже, в перерізі є еліпс.

2)При перерізі площиною xOz 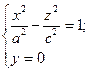– в перерізі - гіпербола.

3)При перерізі площиною zOy 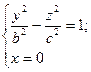– в перерізі – гіпербола.

4) Розглянемо переріз, утворений в результаті перетину деякою некоординатною площиною. Наприклад, z=p.

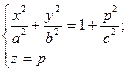
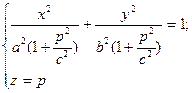
Це рівняння еліпса з півосями 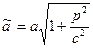, 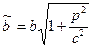. При зростанні ці півосі зростають.

Однопорожнинний гіперболоїд має три площини симетрії (координати в рівнянні мають другий степінь), які в даному випадку співпадають з координатними.

Якщо a=b, то 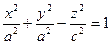- ми отримуємо гіперболоїд як поверхню обертання гіперболи .

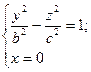Двопорожнинний гіперболоїд - це поверхня, рівняння якої в деякій вибраній системі координат має вигляд: .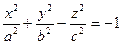

Проведемо дослідження його форми.

1) При перерізі площиною xOy 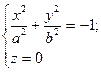, площина поверхню

не перетинає (кажуть, що в перетині уявний еліпс).

2) При перерізі площиною xOz 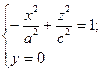– в перерізі - гіпербола.

3) При перерізі площиною zOy 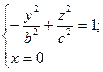– в перерізі – гіпербола.

4) Розглянемо переріз, утворений в результаті перетину деякою некоординатною площиною. Наприклад, z=p.

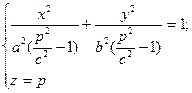
При 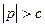отримаємо еліпс з півосями 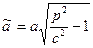, 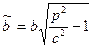. При зростанні ці півосі зростають.

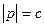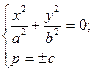Якщо , то - отримаємо дві точки.

Випадок 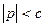аналогічний випадку 1).

Двопорожнинний гіперболоїд має три площини симетрії (координати в рівнянні мають другий степінь), які в даному випадку співпадають з координатними.

(Малюнок див. нижче)

4. Конус другого порядку -це поверхня, рівняння якої в деякій вибраній системі координат має вигляд: .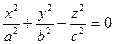

Проведемо дослідження його форми.

1) При перерізі площиною xOy 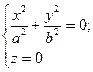, площина поверхню перетинає лише в точці О(0;0;0).

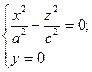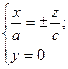2) При перерізі площиною xOz Ю – в перерізі – пара прямих.

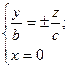3) При перерізі площиною zOy Ю – в перерізі – пара прямих.

Розглянемо переріз, утворений в результаті перетину деякою площиною z=p.

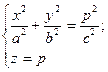
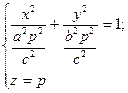– еліпс

При зростанні півосі еліпса зростають.

При a=b, отримаємо круговий конус.

Конус- поверхня обертання, отримана внаслідок обертання прямої навколо осі Oz.

Можна показати, що конус другого порядку є асимптотичною поверхнею для відповідних одно- та двопорожнинних гіперболоїдів.

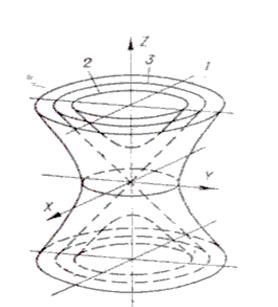
На малюнку справа

1- однопорожнинний гіперболоїд;

2- двопорожнинний гіперболоїд;

3- їх напрямний конус.

Дата добавления: 2014-01-13