Понятие о параметрическом и стохастическом программировании

Параметрическое программирование. В экономической практике нередко возникают задачи, в математических моделях которых коэффициенты линейной формы или системы ограничений (или те и другие) не являются постоянными числами, а меняются в зависимости от некоторых параметров. Напри мер, в задаче об оптимальном использовании ресурсов (оптимальном планировании производства) прибыль от реализации (или цена) продукции может носить сезонный характер и являться функцией времени, а запасы ресурсов и технологические коэффициенты (выражающие размеры их потребления на единицу продукции каждого вида) могут изменяться в зависимости от времени, технологии производства, вместимости складских помещений и т. п.

Параметрическое программирование рассматривает экстремальные задачи с целевыми функциями и ограничениями, зависящими от параметров, разрабатывает методы нахождения оптимальных решений для совокупностей значений параметров и изучает поведение оптимальных планов этих задач при изменении параметров.

Наиболее простой и хорошо изученной является задача линейного параметрического программирования с одним параметром, от которого зависят только коэффициенты целевой функции. Эта задача состоит в максимизации линейной функции 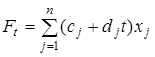, при ограничениях 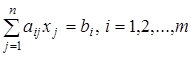и условии неотрицательности переменных x_j ³ 0 (j = 1,..., n), где c_i, d_j, a_ij, b_i — заданные постоянные, а t — параметр, изменяющийся в пределах от a до b: t Î [a; b].

В результате решения задачи (если таковое существует) отрезок [a; b] разбивается на конечное число отрезков значений параметра t таким образом, чтобы для каждого из них максимальное значение линейной функции F_t достигалось в одной и той же вершине многогранника решений. Тем самым для каждого промежутка значений параметра находится оптимум и оптимальное решение.

Стохастическое программирование представляет собой совокупность методов решения оптимизационных задач вероятностного (стохастического) характера. Задача об оптимальном использовании ресурсов, транспортная задача и т. п. становятся задачами стохастического программирования, если параметры целевой функции либо системы ограничений (или и те и другие) рассматривать как случайные величины. В стохастической постановке эти задачи будут полнее отображать экономическую действительность.

При решении стохастических задач проще всего найти средние значения всех случайных параметров и свести такие задачи к обычным, детерминированным задачам математического программирования. Однако такой подход не всегда эффективен, так как при некоторых реализациях случайных величин (параметров) можно прийти к решению, далекому от оптимального, или даже к отсутствию решений задачи.

Другой подход состоит в том, что на первом этапе устанавливается предварительный оптимальный план на основе решения детерминированной задачи, который и реализуется на этом этапе. Затем на втором (последующих) этапе этот план корректируется в соответствии с реальными статистическими характеристиками параметров. Так поступают, например, при решении задачи об оптимальном использовании ресурсов, транспортной задачи при неопределенном спросе на продукцию.

Дата добавления: 2014-01-13