Принятие решений в условиях неопределенности

Одним из определяющих факторов в таких задачах является внешняя среда или природа, которая может находиться в одном из состояний , …, , 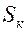которое неизвестно лицу, принимающему решение (наблюдатель).

Пусть по–прежнему , полезность результата при использовании стратегии 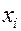. В зависимости от состояния среды результат 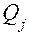достигается с вероятностью .

Кроме того, наблюдателю неизвестно распределение вероятностей . Относительно среды наблюдатель может высказывать определенные гипотезы. Его предположение о вероятном состоянии среды называется субъективными вероятностями 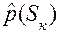. Если бы величина 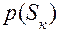была известна наблюдателю, то мы бы имели задачу принятия решений в условиях риска. В этом случае решающее правило 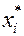определяется следующим образом:

(6.5)

Но на самом деле состоярие среды, а также распределение вероятностей неизвестно.

Как выбрать оптимальную стратегию при этом? Существует несколько критериев для выбора оптимальной стратегии.

а) Критерий Вальда (критерий осторожного наблюдателя). Этот критерий оптимизирует полезность в предположении, что среда находится в самом невыгодном для наблюдателя состоянии. При этом критерии решающее правило имеет вид:

(6.6)

где (6.7)

По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем состоянии среды.

б) Критерий Гурвица основан на следующих предположениях: среда может находиться в самом невыгодном состоянии с вероятностью 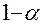и в самом выгодном – с вероятностью 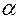, где 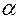– коэффициент доверия. Тогда решающее правило записывается так:

(6.8)

Если , то получаем критерий Вальда.

Если , то приходим к решающему правилу вида

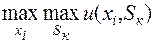(6.9)

так называя стратегию «здорового оптимизма», который верит в удачу.

в) Критерий Лапласа. Если неизвестны состояния среды, то все состояния среды считают равновероятными.

В результате решающее правило определяется соотношением (6.8) при условии .

г) Критерий Сэвиджа (критерий минимизации сожалений).

«Сожаление» – это величина, равная изменению полезности результата при данном состоянии среды относительно наилучшего возможного состояния.

В этом случае критерий для выбора оптимальной стратегии имеет следующий вид:

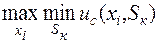(6.10)

где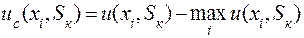

Выбор критерия принятия решения является наиболее сложным и ответственным этапом в системном анализе. При этом не существует каких–либо общих рекомендаций или советов. Выбор критерия должен производить заказчик на самом высоком уровне и в максимальной степени согласовывать этот выбор с конкретной спецификой задачи, а также со своими целями.

В частности, если даже минимальный риск недопустим, то используют критерий Вальда. Если, наоборот, определенный риск вполне приемлем и заказчик готов вложить в некоторое предприятие столько средств, чтобы он потом не сожалел, что вложено мало, то выбирают критерий Сэвиджа.

Условия оценки эффективности систем для неопределенных операций можно представить в виде таблицы.

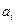
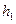
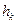
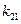
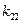
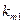
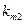
Здесь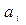– значение вектора управляемых параметров, определяющий свойства системы ;

– значение вектора неуправляемых параметров, определяющий состояние обстановки;

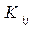– значение эффективности значения для состояния обстановки ;

– эффективность системы .

В зависимости от характера неопределенности операции могут делиться на игровые и статистические неопределенные.

В игровых операциях неопределенность вносит своими сознательными действиями противник. Как в этом случае находится оптимальное решение, мы рассматривали в п.7.

Условия статистически неопределенных операций зависят от объективной действительности, называемой природой. В этом случае применяется теория статистических решений.

Единого критерия оценки эффективности для неопределенных операций не существует. Разработаны лишь общие требования к критериям оценки и выбора оптимальных систем. Основными требованиями являются:

1. оптимальное решение не должно меняться с перестановкой строк и столбцов матрицы эффективности;

2. оптимальное решение не должно меняться при добавлении тождественной строки или столбца к матрице эффективности;

3. оптимальное решение не должно меняться от добавления постоянного числа к значению каждого элемента матрицы эффективности;

4. оптимальное решение не должно становиться неоптимальным и, наоборот, в случае добавления новых систем, среди которых нет ни одной более эффективной системы;

5. если система и оптимальны, то вероятностная смесь этих систем тоже должна быть оптимальна.

В зависимости от характера предпочтений ЛПР наиболее часто в неопределенных операциях используются критерии:

а) среднего выигрыша;

б) Лапласа;

в) осторожного наблюдателя (Вальда);

г) максимакса;

д) пессимизма–оптимизма (Гурвица);

е) минимального риска.

Пример: Необходимо оценить один из трех разрабатываемых программных продуктов для борьбы с одним из четырех типов программных воздействий .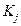

Пусть дана матрица эффективности (рис. 14.2)

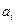
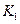
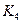
	0,1	0,5	0,1	0,2
	0,2	0,3	0,2	0,4
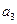
	0,1	0,4	0,4	0,3

Рис. 14.2

Здесь – программный продукт – оценка эффективности применения программного продукта при программном воздействии .

а) критерий среднего выигрыша.

Данный критерий предполагает задание вероятностей состояний обстановки . Эффективность систем оценивается как т.е.

Оптимальной системы будет соответствовать эффективность

Пусть в нашем случае . Тогда

Оптимальное решение – система .

б) критерий Лапласа.

В основе критерия лежит предположение: поскольку о состоянии обстановки ничего не известно, то их можно считать равновероятностными. Исходя из этого:

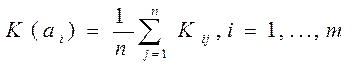
В нашем случае

Оптимальное решение – система a₃. Критерий Лапласа представляет собой частный случай критерия среднего выигрыша.

в) критерий осторожного наблюдателя (Вальда) – это максиминный критерий, он гарантирует определенный выигрыш при наихудших условиях.

Оптимальной считается система из строки с максимальным значением эффективности:

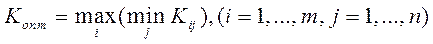
В нашем случае

Оптимальное решение – система .

Максиминный критерий ориентирует на решение, не содержащее элементов риска; в этом его недостаток, другой – он не удовлетворяет условию 3.

г) критерий максимакса.

Критерий максимакса – самый оптимистический критерий. Те, кто предпочитают им пользоваться, всегда надеются на лучшее состояние обстановки, и естественно, в большей степени рискуют.

В нашем случае

Оптимальное решение – система .

д) критерий пессимизма – оптимизма (Гурвица).

Это критерий обобщенного максимина. Для этого вводится коэффициент оптимизма , характеризующий отношение к риску лица, принимающего решение. Эффективность систем находится как взвешенная с помощью коэффициента сумма максимальной и минимальной оценок:

Условие оптимальности записывается в виде

Пусть и рассчитаем эффективность систем для рассматриваемого примера:

Оптимальное системой будет.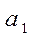

При критерий Гурвица сводится к критерию максимина, при – к критерию максимакса. На практике пользуются значениями коэффициента 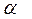в пределах 0,3–0,7. В критерии Гурвица не выполняются требования 4 и 5.

е) критерий минимального риска (Сэвиджа).

Этот критерий минимизирует потери при наихудших условиях.

Преобразуем матрицу эффективности в матрицу потерь (риска), в которой элементы определяются соотношением:

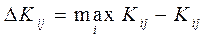
И используем критерий минимакса:

Обратимся опять к рассматриваемому примеру. В нем матрице эффективности будет соответствовать матрица потерь:

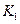
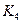
	0,1		0,3	0,2
		0,2	0,2
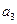
	0,1	0,1		0,1

Тогда

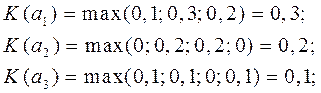
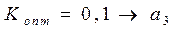
О критерии Сэвиджа можно сказать, что в нем по сравнению с критерием Вальда придается несколько большее значение выигрышу, чем проигрышу. Основной недостаток критерия – не выполняется требование 4.

Таким образом, эффективность систем в неопределенных операциях может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:

а) природа конкретной операции и ее цель (в одних операциях допустим риск, в других – важен гарантированный результат);

б) причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели);

в) характер лица, принимающего решения (одни люди склонны к риску, в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).

Дата добавления: 2014-01-13