Геометрична інтерпретація задачі лінійного програмування

Лекція 4

Задача лінійного програмування має наочне геометричне уявлення, коли кількість змінних не перебільшує трьох. При двох змінних геометричне уявлення можна побудувати на площині, а при трьох – у трьохвимірному просторі.

Розглянемо побудову геометричної інтерпретації на прикладі задачі, математична модель якої має такий вигляд.

F = 7x₁ + 5x₂ max,

2x₁ + x₂ £ 8,

4x₁ + 5x₂ £ 20,

3x₁ + 8x₂ £ 24,

x₁, x₂ ³ 0.

Кожній упорядкованій парі значень (x₁, x₂) ставлять у відповідність точку на площині з прямокутною системою координат. На цій площині визначають допустиму область – множину точок, що задовольняють усім обмеженням задачі. Для цього послідовно розглядають усі обмеження.

Оскільки згідно з обмеженнями змінні можуть приймати тільки невід’ємні значення, допустима область розташовується у першому квадранті.

Знайдемо область, у якій усі точки задовольняють першому непрямому обмеженню. Точки, що задовольняють рівнянню 2x₁ + x₂ = 8, утворюють пряму, положення якої можна визначити по точках перетинання з вісями координат. Координати точки перетинання з віссю x₁ визначаються при підстановці x₂ = 0 у це рівняння. Маємо 2x₁ = 8, або x₁ = 4. Координати точки перетинання з віссю x₁ - (4, 0). Аналогічно підстановкою x₁ = 0 визначаємо координати точки перетинання з віссю x₂ - (0, 8). Розташування прямої показано на мал.4.1.

Для того, щоб визначити, де розташовані точки, для яких виконується умова 2x₁ + x₂ < 8, розглянемо довільну точку A на побудованій прямій. Для точок, що розташовані лівіше або нижче точки A, ліва частина обмеження має

x₂ 8 - 7 - 6 - 5 - 4 - 3 - A(x_1A, x_2A) 2 - x₁ < x_1A 1 - x₂ < x_2A x₁ 0 1 2 3 4 5 6 7 8

Мал.4.1. Визначення області виконання

обмеження 2x₁ + x₂ £ 8.

менше значення, і нерівність виконується, а для точок, розташованих правіше або вище, - не виконується. Таким чином, побудована пряма поділяє усю координатну площину на дві напівплощини: у одній обмеження виконується, а у іншій – ні.

x₂ 8 - 7 - 6 - 5 - 4 - grad F 3 - 2 - A B K 1 - O C D E x₁ 0 1 2 3 4 5 6 7 8

Мал.4.2. Визначення допустимої області

задачі.

Для визначення напівплощини, у якій виконується обмеження, достатньо у ліву частину підставити координати довільної точки, що не лежить на прямій, і порівняти отримане значення з правою частиною. Найпростіше використовувати початок координат. У прикладі підстановка x₁ = 0, x₂ = 0 дає нульове значення лівої частини, і оскільки 0 £ 8, у напівплощині, що містить початок координат, обмеження виконується. Будемо стрілочкою вказувати напівплощину виконання обмеження (мал.4.1).

Аналогічно можна побудувати області виконання інших непрямих обмежень і отримати допустиму область задачі як перетинання побудованих областей (мал.4.2). Отже допустима область у прикладі являє собою п’ятикутник OABCD.

Тепер задача полягає у пошуку у п’ятикутнику OABCD точки, у якій функція F = 7x₁ + 5x₂ приймає максимальне значення. Для розв’язування цієї задачі з’ясуємо поведінку функції F у допустимій області. Поведінка функції n змінних “у малому”, тобто при незначних змінах аргументів, визначається її диференціалом

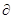
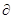
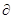
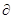
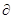
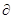dF = F/ x₁ dx₁ + F/ x₂ dx₂ + … + F/ x_n dx_n.

Праву частину можна уявити як скалярний добуток двох векторів: координати першого вектору – частинні похідні функції F, а координати другого – диференціали незалежних змінних. Вектор, координати якого дорівнюють частинним похідним деякої функції f, називається градієнтом цієї функції і позначається як grad f. Вектор, координати якого дорівнюють диференціалам незалежних змінних, будемо називати вектором прирісту аргументу і позначати як dx. Таким чином

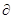
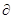
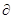
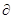
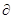
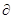grad F = (F/ x₁, F/ x₂, …, F/ x_n),

dx = (dx₁, dx₂, …, dx_n),

dF = (grad F, dx). (4.1)

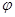
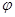Вибір різних значень dx_i при зберіганні значення |dx| відповідає просуванню від поданної точки допустимої області на фіксовану відстань у різних напрямках. Кожному просуванню відповідає зміна значення цільової функції F, а головна лінійна частина цієї зміни дорівнює dF. Тому при незначних просуваннях найбільше зростання функції має місце у тому напрямку, у якому dF приймає найбільше значення. З формули (4.1) випливає, що dF максимальне, коли напрямки векторів grad F і dx співпадають, оскільки (grad F, dx) = |grad F| |dx| cos, де - кут між векторами grad F і dx.

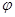
Отже grad F вказує напрямок найбільшого зростання функції F. Разом з тим, формула (4.1) показує, що коли cos = 0 (= /2), dF = 0, тобто функція F не змінюється. Лінія, яка у кожній точці перпендикулярна до градієнту, називається лінією рівня. Лінія рівня – це множина точок, у яких цільова функція має постійне значення (для кожної лінії своє).

У випадку розв’язування задачі лінійного програмування в усіх точках допустимої області градієнт цільової функції має стале значення – координати градієнту дорівнюють коефіцієнтам цільової функції.

Після визначення градієнту цільової функції (мал.4.2) залишається знайти у допустимій області точку, від якої неможливо зсунутися у напрямку градієнту, залишаючись у допустимій області. Пошук такої точки зручно здійснюється за допомогою лінії рівня. У випадку двовимірної задачі лінія рівня являє собою пряму перпендикулярну до градієнту. На мал.4.2 лінії рівня показані штриховими прямими. Для пошуку розв’язку задачі довільну лінію рівня, зберігаючи її нахил до вісєй координат, зсовують у напрямку градієнту, доки вона має спільні точки з допустимою областю. Граничне положення і визначає розв’язок. У поданому прикладі розв’язком задачі є координати точки C.

Для визначення координат точки C, враховучи, що ця точка лежить на перетинанні прямих 1 і 2, з системи рівнянь

2x₁ + x₂ = 8,

4x₁ + 5x₂ = 20;

отримуємо розв’язок задачі х₁ = 10/3, x₂ = 4/3. Максимальне значення цільової функції визначаємо підстановкою розв’язку у вираз для цільової функції.

F_max = 7 * 10/3 + 5 * 4/3 = 30.

Дата добавления: 2014-01-13