Аналіз залежності розв’язку задачі від правих частин обмежень

Аналіз залежності розв’язку задачі від параметрів

Розв’язану задачу лінійного програмування можна розглядати як модель деякої задачі про розподіл ресурсів. Наприклад, ця модель могла бути побудована для розв’язування такої практичної задачі про розподіл ресурсів.

Деяка конфетна фабрика виготовляє два види цукерок – “тузики” і “білочки”. Ціна на “тузики” становить 7 грн, а на “білочки” – 5 грн. Для виготовлення 1 кг “тузиків” витрачається 2 кг цукру, 4 кг какао та 3 кг горіхів, а для 1 кг “білочок” – 1 кг цукру, 5 кг какао і 8 кг горіхів. Добові запаси цукру, какао та горіхів відповідно складають 8, 20 і 24 кг. Треба визначити добові об’єми виготовлення обох видів цукерок, при яких сумарна вартість продукції максимальна.

Знайдений розв’язок задачі лінійного програмування вказує, який план фабрики буде оптимальним при сталих параметрах (ціни – коефіцієнти цільової функції, об’єми запасів – праві частини обмежень, витрати сировини на виготовлення одиниці продукції – коефіцієнти обмежень). На практиці важливо також знати, як змінеться оптимальний план при змінах параметрів моделі, тобто знати динамічні характеристики моделі.

Розглянемо аналіз чутливості моделі до зміни запасів ресурсів. При цьому аналізі розглядаються такі питання.

1. На скільки можна збільшити запас ресурсу для покращення значення цільової функції?

2. На скільки можна зменшити запас ресурсу без погіршення значення цільової функції?

3. Збільшення запасу якого ресурсу найбільш доцільне?

Обмеження, що при оптимальному наборі значень змінних приймають вигляд рівнянь, називають зв’язуючими, а відповідні ресурси – дефіцитними. Інші обмеження називать незв’язуючими, і відповідні ресурси – недефіцитними.

У прикладі, що розглядається, перший і другий ресурси дефіцитні, а третій – ні.

Збільшення запасу i-го ресурсу викликає зсув прямої l_i, відповідаючої цьому ресурсу, у напрямку градієнту лівої частини i-го обмеження. Якщо i-й ресурс недефіцитний, точка-розв’язок не лежить на прямій l_i, і її зсув не впливає на оптимальне значення цільової функціїї, доки пряма l_i не пройде через цю точку. Цією умовою визначається граничне зменшення запасу недефіцитного ресурсу.

Якщо i-й ресурс дефіцитний, точка-розв’язок лежить на прямій l_i, і її зсув призводить до зсуву цієї точки. При цьому покращення значення цільової функції можливе, доки пряма, що зсовується, має спільні точки з допустимою областю. Граничне збільшення запасу визначається граничним положенням прямої, що зсовується.

У прикладі граничне зменшення запасу недефіцитного третього ресурсу визначається умовою, проходження прямої 3 через точку C. Для визначення відповідного запасу b^’₃ підставляємо координати точки C у ліву частину третього обмеження: b^’₃ = 3 * 10 / 4 + 8 * 3 / 4 = 27 / 2. Зміна запасу ресурсу становить b₃ = b^’₃ - b₃ = 27 / 2 – 24 = - 21 / 2.

Збільшення запасу першого ресурсу пов’язане із зсувом прямої 1 у бік збільшення допустимої області. При цьому, доки оптимальна точка переміщується по відрізку CE, значення цільової функції збільшується. При подальшому збільшенні запасу пряма 1 не має спільних точок з допустимою областю, яка має вигляд чотирикутника OABE, і значення цільової функції не змінюється. Тому максимальне збільшення запасу першого ресурсу визначається умовою належності точки E прямій 1. Підставляючи координати точки E у ліву частину першого обмеження, отримуємо

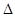b^’₁ = 2 * 5 + 1 * 0 = 10, b₁ = b^’₁ - b₁ = 10 – 2 = 2.

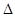Відповідне максимальне значення цільової функції визначається підстановкою координат точки E у вираз для цільової функції: F^’_max1 = 7 * 5 + 5 * 0 = 35, і збільшення значення цільової функції становить F_max1 = F^’_max1 - F_max = 35 – 30 = 5.

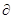
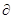Цінністю i-го ресурсу називають величину p_i = F_max / b_i. Для задачі лінійного програмування цінність – це збільшення максимального значення цільової функції, відповідаюче одиничному збільшенню запасу ресурсу, або відношення збільшення максимального значення цільової функції до відповідного збільшення запасу ресурсу.

Отже цінність першого ресурсу дорівнює p₁ = 5/2.

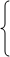Для другого ресурсу граничне збільшення запасу визначається точкою K, координати якої визначаються з системи

2x₁ + x₂ = 8,

3x₁ + 8x₂ = 24;

і становлять x₁ = 40/13, x₂=34/13. Підставляючи отримані координати у відповідні вирази, маємо

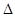b^’₂ = 4 * 40/13 + 5 * 24/13 = 280/13, b₂ = b^’₂ - b₂ = 280/13 – 20 = 20/13,

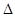F^’_max2 = 7 * 40/13 + 5 * 24/13 = 400/13, F_max2 = F^’_max2 - F_max = 400/13 – 30 = 10/13,

p₂ = 1/2.

Табл.4.1

Ресурс	Статус	Макс. зб. зап.	Зб. ціл. функц.	Цінність
	деф.			5/2
	деф.	20/13	10/13	1/2
	недеф.	-10/3

Отримані результати дослідження залежності розв’язку задачі від правих частин обмежень зведені у табл.4.1.

Аналіз залежності розв’язку задачі від коефіцієнтів цільової функції

У цій задачі розглядаються такі питання.

1. Який діапазон зміни того чи іншого коефіцієнта цільової функції, при якому не змінюється оптимальний розв’язок задачі?

2. Наскільки слід змінити той чи інший коефіцієнт цільової функції, щоб зробити деякий недефіцитний ресурс дефіцитним і, навпаки, дефіцитний ресурс зробити недефіцитним

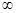
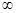Зміна одного з коефіцієнтів цільової функції призводить до повороту градієнту і відповідного повороту лінії рівня. При цьому градієнт завжди залишається у одній напівплощині, що визначається значенням коефіцієнту, що не змінюється. Так, при зміні від - до коефіцієнту c₁ (при змінній x₁) у прикладі, що розглядається, координата x₂ градієнту зберігає значення 5, і градієнт залишається у верхній напівплощині, обертаючись за годинковою стрілкою від положення, наближеного до від’ємної напіввісі x₁, до положення, наближеного до додатньої напіввісі x₁.

Аналізуючи графічне уявлення допустимої області задачі, можна переконатися, що при вказаному обертанні градієнту оптимальна точка послідовно приймає положення точок A, B, C і D. Залишається визначити значення коефіцієнту c₁, при яких відбувається перехід від однієї точки до іншої.

З геометричної інтерпретації задачі ясно, що шукані значення коефіцієнту відповідають одночасній оптимальності суміжних (з’єднаних відрізком межі допустимої області) точок. Так, перехід від точки A до B відбувається, коли лінія рівня паралельна відрізку [A, B], від B до C – при паралельності лінії рівня відрізку [B, C], а від C до D - відрізку [C, D]. Умовою паралельності прямих є пропорційність коефіцієнтів при змінних у рівнянні. Для ліній рівня цими коефіцієнтами є коефіцієнти цільової функції, а для відрізків межі допустимої області – коефіцієнти у лівих частинах відповідних обмежень.

Значення коефіцієнту c₁, при якому відбувається перехід від точки A до B знаходимо з рівняння c_1AB/3 = 5/8, і отримуємо c_1AB = 15/8. Для переходу від B до C маємо c_1BC/4 = 5/5, c_1BC = 4, а від C до D - c_1CD/2= 5/1, і c_1CD = 10.

Табл.4.2

Ресурс	Діапазони с1 (-,15/8) (15/8,4) (4,10) (10,)
	недеф.	недеф.	деф.	деф.
	недеф.	деф.	деф.	недеф.
	деф.	деф.	недеф.	недеф.

Для кожного положення оптимальної точки очевидним чином визначається статус ресурсів. Тому результати дослідження залежності розв’язку задачі від коефіцієнту c₁ цільової функції можна звести у табл.4.2.

Аналогічно можна скласти таблицю і для с₂. Зрозуміло, що отримані таблиці містять достатню інформацію для відповіді на сформульовані вище питання аналізу залежності розв’язку задачі від коефіцієнтів цільової функції.

Дата добавления: 2014-01-13