Задачи линейного программирования. Лекция 5.2. Методы оптимизации на компьютерных моделях

Лекция 5.2. Методы оптимизации на компьютерных моделях.

Модуль 5. Оптимизация систем автоматизации на моделях

Экономические задачи привели к возникновению линейного программирования. Большинство экономических моделей являются линейными, например, задачи:

- оперативного планирования;

- объемного планирования;

- снабжения и перевозок;

- управления запасами и др.

В экономических задачах переменные интерпретируются как цены на ресурсы и продукцию. Для этих задач характерна высокая размерность (сотни и тысячи переменных).

Технические задачи линейного программирования:

- задача составления шихт для агломерации, коксования, производства чугуна и стали;

- обнаружение и устранение неисправностей,

- раскрой материалов.

Математические постановки задач линейного программирования могут отличаться лишь ограничениями.

Виды задач линейного программирования:

1.Общая задача линейного программирования - определение набора значений варьируемых переменных Х_J, при которых достигается максимум или минимум линейной целевой функции

F(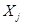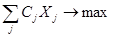₎ =(min), 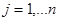(1)

при условиях - ограничениях в виде равенств

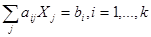(2)

и в виде неравенств

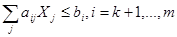(3)

При этом обязательно соблюдаются условия неотрицательности оптимальных значений варьируемых переменных:

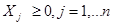(4)

Любое решение, удовлетворяющее системе ограничений, является допустимымрешением (допустимым планом). Допустимое решение, доставляющее минимум (максимум) целевой функции - оптимальноерешение.

2. Стандартная (симметричная) задача линейного программирования - определение максимума целевой функции при ограничениях, заданных в виде неравенств.

3. Каноническая (основная) задача линейного программирования - определение максимума при ограничениях заданных в виде равенств.

Эти три задачи могут быть преобразованы одна в другую. Необходимое преобразование зависит от выбранного метода решения. Для преобразования видов задач нужно:

1. свести задачу минимизации к задаче максимизации:

min F=-max(-F)

2. преобразовать ограничения типа неравенств:

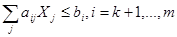(3)

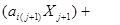в равенства 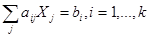(2)

Вводимые дополнительные переменные имеют экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражены расходы и наличие производственных ресурсов, то дополнительная переменная - неиспользуемый ресурс.

3. преобразовать все переменные в неотрицательные:

если X_k не подчинена условиям неотрицательности, то она заменяется двумя неотрицательными переменными:

X_k = U_k - V_k

Дата добавления: 2014-01-13