Геометрический метод решения

Решим задачу:

F=c₁ X₁+ c₂ X₂® max

при условии

a_i1 X₁+ a_i2 X₂ £ b_i

Каждое неравенство определяет полуплоскость с граничными прямыми a_i1 X₁+ a_i2 X₂ = b_i (i=1,…k), а условия неотрицательности определяю положение области допустимых планов в первом квадранте. Если система ограничений совместна, то область решений есть множество точек, принадлежащих указанным полуплоскостям. Область допустимых решений лежит в многоугольнике, образованном ограничениями - неравенствами.Для пространства, когда параметров больше двух, многоугольник превращается в многогранник.. или в гипермногогранник. Поскольку целевая функция является функцией от x,y, то даже для двух варьируемых параметров задача становиться трехмерной.

Многогранник решений в задачах линейного программирования всегда выпуклый. Это значит, что между любыми двумя его точками можно провести прямую, не пересекающую его границу..Максимум (минимум) целевой функции всегда находится в вершинах многогранника решений, или на его грани, или на одной из ограничивающих его гиперплоскостей.

Задача линейного программирования сводится к поиску вершины, где целевая функция минимальна или максимальна.

Последовательность решений:

1. на координатной плоскости строят прямые, соответствующие границам неравенств;

2. отштриховывают соответствующие полуплоскости;

3. строят многоугольник ограничений;

4. строят прямую F(X₁ , X₂) =h (h -произвольное);

5. передвигают прямую параллельно себе в направлении, соответствущем увеличению или уменьшению h, до касания с крайней точкой многоугольника ограничений. Эта точка соответствует оптимальному плану.

6. определяют значение параметров оптимального плана, т.е. _X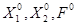

Геометрический метод работает при 2-3 переменных. При увеличении размерности в разумных пределах определяют все вершины n-мерного многогранника решений, вычисляют целевую функцию в этих вершинах, а потом сравнивают их путем полного перебора. Это метод полного перебора вершин.

СИМПЛЕКС - МЕТОД РЕШЕНИЯ

Симплекс - метод использует ту же идею, что и предыдущие методы (оптимальное решение находится в одной из вершин), но в нем

- просмотр вершин ведется по соседним вершинам;

- просмотр ведется таким образом, что значение целевой функции возрастает шаг за шагом (для задач максимизации),

Схема метода:

1. принимаем в качестве начального приближения координату любой вершины;

2. находим все ребра, выходящие из нее;

3. определяем "наклоны" всех ребер;

4. двигаемся вдоль того ребра, где целевая функция возрастает быстрее, и приходим в новую вершину;

5. далее процедура повторяется до прихода в максимальную вершину, движение из нее по любому ребру приводит к убыванию целевой функции.

Данный метод применяется:

1. для пространств любой размерности;

2. всегда дает оптимальное решение за n или 2n шагов;

3. оптимальное решение на выпуклом многограннике ограничений всегда

единственно.

Практически для решения задач используют готовые программы. Кроме поиска оптимального плана, эти пакеты программ позволяют произвести анализ решения:

определить в каких пределах могут меняться коэффициенты целевой функции, чтобы оптимальный план еще сохранялся;

оценить устойчивость оптимального плана к изменению коэффициентов и свободных членов системы уравнений - ограничений.

.

Дата добавления: 2014-01-13