Метод Гаусса — Зайделя

Метод Гаусса — Зайделя (в математической литературе ис­пользуется и другое название — метод покоординатного спуска) заключается в последовательном поиске оптимума R(x) пооче­редно по каждой переменной. Причем после завершения перебора всех переменных (т.е. после завершения одного цикла) опять в общем случае приходится перебирать все переменные до тех пор, пока не придем к оптимуму.

В ряде случаев (для сепарабельных критериев оптимальности, т.е. таких R(x₁, x₂,,..,x_i,...,х_n), которые можно представить в виде

удается получить решение всего за один цикл. В случае тесной нелинейной взаимосвязи переменных (например, при наличии произведения переменных и т.п.) для получения решения приходится делать очень много циклов.

Метод обладает низкой эффективностью в овражных функциях, может застревать в "ловушках", особенно при сравнительно больших шагах h при поиске оптимума по каждой переменной, очень чувствителен и к выбору системы координат. Метод прост в реализации. На эффективность метода влияет порядок чередо­вания переменных.

Условием окончания поиска является малость изменения критерия оптимальности за один цикл или невозможность улучшения критерия оптимальности ни по одной из переменных.

В двумерных задачах метод Гаусса — Зайделя фактически сводится к методу наискорейшего спуска, так как в обоих методах траектория поиска представляет собой последовательность вза-имноортогональных отрезков.

МНОГОМЕРНАЯ УСЛОВНАЯ ОПТИМИЗАЦИЯ

В данном разделе рассматриваются численные методы построения улучшающих последовательностей при наличии огра­ничений типа равенств (связей) и типа неравенств (ограничений) (рис. 20). Сюда не входят методы, использующие условия оптимальности. Во всех методах строится в допустимой области последовательность точек, в которых значения критерия улучшаются. Поиск осуществляется градиентным методом. При этом предполагается, что учащийся знаком с особенностями и усло­виями работы этого метода по крайней мере в объеме соответ­ствующего раздела настоящего пособия.

Допустимая область может формироваться автономными ог­раничениями

X_{i min} £ X_i £ X_{i max},

связями f (x₁, x₂,..., x_n) = 0 (j = 1,..., т)

и. ограничениями F_j(x₁, x₂,..., x_n) ³ 0, для j = 1,..., p.

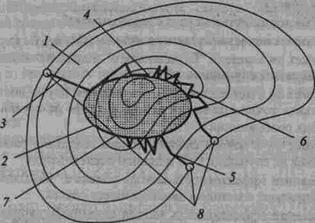
Рис. 20. Иллюстрация траекторий поиска минимума функции при наличии ограничений типа неравенств: 7 — допустимая область; 2 — запрещенная область; 3 — траектория метода проектирования градиента; 4 — оптимум 1; 5 — траектория метода штрафов; 6 — траектория прямого метода с возвратом; 7 — оптимум 2; 8 — начальные течки поиска

Функции, задающие ограничения, могут формировать допустимую область с различными свойствами: монотонными, колебательными, с большой и малой кривизной и т.д., что оказывает влияние на эффективность методов поиска.

Дата добавления: 2014-01-13