Опукла оболонка є прикладом опуклої множини

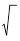
Відстанню d(a, b) між двома точками а = (а_1, а_2, …, a_n) та b = (b_1, b_2, …, b_n) називають довжину вектору a – b: d(a, b) = (a-b, a-b) = (а_j - b_j) ².

Кулею S_c^r радіуса r з центром у точці c називаєтья множина усіх точок х таких, що відстань d(x, c) £ r: S_c^r = {x | d(x, c) £ r}.

Множина точок називається обмеженою, якщо вона міститься у кулі скінченного радіусу.

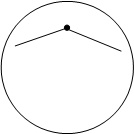
        Мал.5.3. Приклад обмеженої множини.

Прикладом обмеженої множини є п’ятикутник на мал.5.3, а прикладом необмеженої множини може бути напівплощина.

Точка a множини M називається межевою, якщо кожна куля з центром у a містить як точки, що належать M, так і точки, що M не належать. Сукупність усіх межевих точок множини утворює її межу. Множина може містити свою межу чи ні. Наприклад, визначена вище куля містить свою межу, а множина M = {x | d(x, c) < p}, з тією ж межою, свою межу не містить.

Граничною точкою множини M називається границя послідовності точок множини M. Множина точок у n-вимірному лінійному векторному просторі називається замкненою, якщо вона містить усі свої граничні точки.

Можна показати, що кожна межева точка є граничною точкою, і тому замкнена множина завжди містить усі свої межеві точки, зокрема свою межу.

Множина може бути замкнена і необмежена або обмежена і незамкнена. Наприклад, напівплощина, точки якої задовольняють нерівності x₂ 0, являє приклад необмеженої замкненої множини, а напівплощина, якій відповідає нерівність x₂ > 0, - необмеженої, незамкненої множини. Розглянута вище множина M = {x | d(x, c) < p} обмежена і незамкнена.

Опукла множина може містити довільну кількість крайніх точок. На мал.5.2 наведено приклад опуклої множини із скінченою ненульовою кількістю крайніх точок. Коло (мал.5.3) має нескінчену кількість крайніх точок – кожна точка межі. Напівплощина не має жодної крайньої точки.

Опуклим многогранником називається обмежена замкнена опукла множина, що містить скінченну кількість крайніх точок. Приклад опуклого многогранника - многокутник на площині.

Дата добавления: 2014-01-13