Властивості задачі лінійного програмування

Надалі будемо розглядати канонічну форму задачі:

F = (c,x) ® min

Ax = b,

x ³ 0.

Будемо вважати, що матриця A містить m рядків і n стовпців, усі рядки матриці A лінійно незалежні, тобто rank (A) = m.

Теорема 5.1 (Про опуклість допустимої області) Допустима область задачі лінійного програмування є опуклою множиною.

Доведення. Нехай u та v – довільні різні допустимі розв’язки задачі. Це означає, що мають місце такі співвідношення

Au = b, Av = b, u ³ 0, v ³ 0.

Розглянемо довільну точку x на відрізку, що з’єднує точки u та v.

x = (1-l)u + lv, 0 £ l £ 1.

Покажемо, що ця точка задовольняє обмеженням задачі.

Ax = A((1-l)u + lv) = Au(1-l) + Avl = b(1-l) + bl = b.

u ³ 0, (1-l) ³ 0 Þ (1-l)u ³ 0.

v ³ 0, l ³ 0 Þ lv ³ 0.

x = (1-l)u + lv ³ 0.

Тому увесь відрізок, що з’єднує u та v, належить допустимій області, що і завершує доведення теореми.

Тепер з’ясуємо питання про кількість крайніх точок у допустимій області.

Теорема 5.2. (Про характерну властивість допустимого базисного розв’язку). Допустимий розв’язок задачі є крайньою точкою тоді і тільки тоді, коли він є базисним розв’язком.

Доведення. Спочатку доведемо достатність умови, тобто частину теореми “тоді”. Нехай x⁰ = (x⁰₁, x⁰₂, …, x⁰_n) допустимий базисний розв’язок. Позначимо через M множину індексів базисних змінних: M = { j | x_j – базисна змінна }. Як і раніше, множину індексів небазисних змінних будемо позначати через N. Будемо вважати, що B – підматриця матриці A, утворена базисними стовпцями. Позначимо x⁰_B вектор, утворений базисними координатами вектору x⁰, і x⁰_N - вектор, утворений небазисними координатами вектору x⁰_N. Для векторів x⁰, x⁰_B і x⁰_N мають місце співвідношення

Ax⁰ = b, x⁰ ³ 0;

Bx⁰_B = b;

x⁰_N = 0.

Доведення проведемо від супротивного. Припустимо, що x⁰ не є крайньою точкою. Тоді існують два різні допустимі розв’язки u = (u₁, u₂, …, u_n) та v = (v₁, v₂, …, v_n), u ¹ v, і x⁰ лежить у середині відрізку [u, v], тобто

x⁰ = (1-l)u + lv, 0 < l < 1.

З останнього векторного рівняння отримуємо систему лінійних рівнянь для небазисних координат векторів u та v

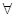0 = (1-l)u_j + lv_j j N. (5.1)

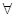
Оскільки u та v допустимі розв’язки, u_j ³ 0 і v_j ³ 0. Крім того, (1-l) > 0 і l> 0. Тому система (5.1) має єдиний розв’язок u_j = v_j = 0 j N.

Як допустимі розв’язки, u та v задовольняють рівнянням

Au = b, Av = b,

а враховуючи, що усі небазисні координати u та v дорівнюють нулю, отримуємо

Bu = b, Bv = b,

де u, v утворені базисними координатами векторів u, v відповідно.

Отже x⁰_B, u та v є розв’язками системи Bx = b, і оскільки B невироджена (система Bx = b має тільки один розв’язок) x⁰_B = u = v. Тому x⁰ = u = v, а це суперечить припущенню і завершує доведення достатності.

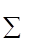Тепер доведемо необхідність. Нехай x⁰ = (x⁰₁, x⁰₂, …, x⁰_n) – крайня точка допустимої області. Знов доведення проведемо від супротивного. Припустимо, що x⁰ не є допустимим базисним розв’язком. Позначимо через N+ множину індексів, для яких координати вектору x⁰ мають додатні значення: N+ = { j | x⁰_j > 0 }. Тоді стовпці матриці A, номери яких належать N+, лінійно залежні, бо інакше x⁰ – допустимий базисний розв’язок. Звідси прямує існування лінійної комбінації стовпців матриці A

l_j a^j = 0, (5.2)

j N+

у якій не усі коефіцієнти дорівнюють нулю.

Побудуємо вектор l^’ = (l^’₁, l^’₂, …, l^’_n) таким чином

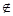
l^’_j = l_j, якщо j N+; l^’_j = 0, якщо j N+.

З (5.2) прямує l^’_j a^j = 0, або Al^’ = 0.

Якщо взяти число p, задовольняюче співвідношенню

0 < p < min { x⁰ _j / | l^’ | },

" l^’ _j ¹ 0

то вектори x¹ = x⁰ + pl^’, x² = x⁰ - pl^’ задовольняють умовам

x¹ ³ 0, x² = ³ 0, Ax¹ = b, Ax² = b.

Дійсно, x¹ = ³ 0, оскільки, якщо l^’_j ³ 0, x¹_j = x⁰_j + pl^’_j ³ 0, як сума невід’ємних величин, а при l^’_j < 0 x¹_j = x⁰_j – p|l^’_j| ³. x⁰_j – (x⁰ _j / | l^’ _j|)|l^’_j| = 0. Для x²_j маємо. При l^’_j £ 0 x²_j = x⁰_j - pl^’_j ³ 0, як сума невід’ємних величин, а при l^’_j > 0 x²_j = x⁰_j – p|l^’_j| ³. x⁰_j – (x⁰ _j / | l^’ _j|)|l^’_j| = 0.

Ax¹ = A (x⁰ + pl^’ ) = Ax⁰ + pAl^’ = b + 0 = b.

Аналогічно, Ax² = b.

Таким чином x¹ і x² - допустимі розв’язки. Вектор x⁰ можна уявити у вигляді x⁰ = 1/2 x¹ + 1/2 x², це суперечить припущенню, що x⁰ - крайня точка, і завершує доведення необхідності.

Остання теорема встановлює еквівалентність понять крайня точка допустимої області задачі лінійного програмування і допустимий базисний розв’язок задачі. Кількість допустимих базисних розв’язків скінчена, оскільки не перевищує кількості базисних розв’язків системи Ax = b, що дорівнює C ⁿ_m. Надалі допустимий базисний розв’язок будемо називати опорним планом. Кожний опорний план являє вершину допустимої області, і, навпаки, кожна вершина – опорний план. З теорем 5.1 і 5.2 прямує, що допустима область задачі лінійного програмування є опуклою множиною із скінченою кількістю крайніх точок.

Дата добавления: 2014-01-13