Если выполняется система линейных ограничений

Линейного программирования

Постановка основной задачи

Имеет наибольшее значение.

Выбрать такое, при котором линейная функция

F=C ₁ х ₁ +C ₂ х ₂ (5.25)

Рассмотренная задача является примером основной зада­чи линейного программирования, представляющей класс оп­тимизационных задач, возникающих на практике. Ясно, что число линейных ограничений в системе (5.24) может быть произвольным.

В общем случае под задачей линейного программирования понимают задачу о нахождении наибольшего или наимень­шего значений линейной функции при наличии линейных ограничений.

При этом линейное ограничение может быть задано либо в виде нестрогого неравенства (как, например, в системе (5.24)), либо в виде равенства (например, a ₁₁ х ₁+ а ₁₂ х ₂ = b ₁,). Функция, наибольшее или наименьшее значение которой разыскивается, называется целевой функ­цией (например, функция (5.25)).

Любая совокупность переменных, удовлетворяющих системе линей­ных ограничений, называется допустимым решением, или допустимым планом.

Допустимое решение называется оптимальным, если при этом достигается наибольшее или наименьшее значение це­левой функции.

Заметим, что число линейных ограничений и число переменных в задаче линейного программирования может быть произвольным. При этом ограничения вида х_i ³ 0,является частным случаем линейного ограничения.

Основная задача ли­нейного программирования с двумя переменными х ₁ и х ₂ ставится следующим образом:

Найти наибольшее (наименьшее) значение линейной це­левой функции: F=C ₁ х ₁ +C ₂ х ₂+ С ₀ (5.26)

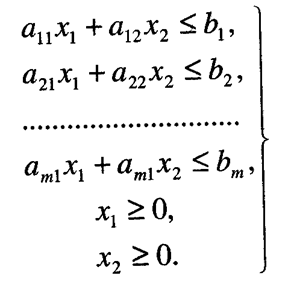(5.26)

Здесь C ₀, C ₁, C ₂, b_i a_ij (i = 1, 2,..., т; j = 1,2) – заданные числа.

Частным случаем такой задачи при т = 4 является рассмот­ренная выше задача об использовании сырья. За­метим, что неравенство со знаком ³ умножением на (–1) заме­няется на неравенство со знаком £.

Основная задача линейного программирования с двумя переменными допускает наглядное решение геометрическим методом, который будет рассмотрен далее.

Дата добавления: 2014-01-13