
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрический метод решения основной задачи линейного программирования
|
|
|
|
Геометрический метод решения основной задачи линейного программирования с двумя переменными основан на следующих теоретических положениях:
1. Наибольшее или наименьшее значение линейная целевая функция (5.26) может принимать только на границе многоугольной области - области решений системы линейных ограничений.
2. Направление вектора 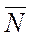 = (С 1 С 2 ) представляет направление наибольшего возрастания целевой функции.
= (С 1 С 2 ) представляет направление наибольшего возрастания целевой функции.
3. Множество точек плоскости, для которых целевая функция F имеет постоянное значение F 0, то есть C 1 х 1 +C 2 х 2+ С 0 = F 0, представляет прямую, перпендикулярную вектору 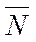 . Множество таких прямых - множество прямых, параллельных друг другу.
. Множество таких прямых - множество прямых, параллельных друг другу.
Алгоритм геометрического метода решения задачи
1. Строим многоугольную область - область решений системы линейных ограничений (5.27).
2. Строим вектор 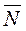 = (С 1 С 2 ) и прямую, перпендикулярную этому вектору.
= (С 1 С 2 ) и прямую, перпендикулярную этому вектору.
3. Перемещаем эту прямую параллельно самой себе в направлении вектора 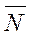 . Первая точка встречи этой прямой с построенной в п. 1 многоугольной областью (точка входа) представляет оптимальное решение, в которой функция F принимает наименьшее значение. Последняя точка (точка выхода) - это оптимальное решение, в которой функция принимает наибольшее значение.
. Первая точка встречи этой прямой с построенной в п. 1 многоугольной областью (точка входа) представляет оптимальное решение, в которой функция F принимает наименьшее значение. Последняя точка (точка выхода) - это оптимальное решение, в которой функция принимает наибольшее значение.
Пример. Найти наибольшее и наименьшее значения целевой функции F = 2 х 1 + 2 х 2, если выполняется система линейных ограничений (5.30).
Решение. Многоугольная область, соответствующая системе (5.30), построена ранее и изображена на рис. 5.11. Построим вектор 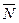 = (2,2) и прямую, перпендикулярную этому вектору (рис. 5.12).
= (2,2) и прямую, перпендикулярную этому вектору (рис. 5.12).
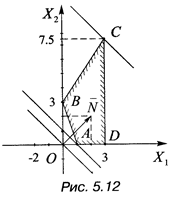
Перемещая эту прямую в направлении вектора 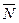 параллельно самой себе, находим точку входа A (1;0) и точку выхода B (3;7,5).
параллельно самой себе, находим точку входа A (1;0) и точку выхода B (3;7,5).
Следовательно, целевая функция достигает наименьшего значения при х 1 = 1 и х 2 = 0 и наибольшего значения при х 1 = 3 и х 2 = 7,5. Эти значения соответственно равны:
F min = F (1;0) = 2×1 + 2×0 = 2,
F max = F (3;7,5) = 2×3 + 2×7,5 = 21.
Пример. Пусть требуется решить задачу об использовании сырья, о которой шла речь в п. 5.5.1, если известна таблица исходных данных:
| Виды сырья | Запасы сырья | Виды продукции | |
| Р 1 | Р 2 | ||
| S 1 | |||
| S 2 | |||
| S 3 | |||
| S 4 | |||
| Доход |
В соответствии со сказанным выше система линейных ограничений представлена в виде:
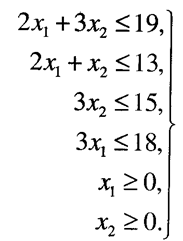 (5.31)
(5.31)
При этом целевая функция имеет вид:
F = 7 x 1 + 5 x 2. (5.32)
Ищем наибольшее значение функции (5.32) при выполнении условий (5.31).
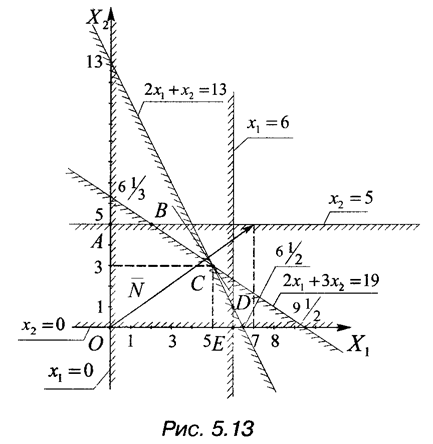
Построим область решения системы (5.31) (рис. 5.13).
Неравенство 2 x 1 + З х 2 £ 19 определяет полуплоскость, ограниченную прямой 2 x 1 + З х 2 =19, или
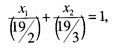
отсекающей на осях координат отрезки 9 ½ и 6 1 / 3, в которой лежит начало координат.
Неравенство 2 x 1 + х 2 £ 13 определяет полуплоскость, ограниченную прямой 2 x 1 + х 2 =13, или 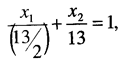
отсекающей на осях координат отрезки 6 ½ и 13, в которой лежит начало координат.
Неравенство 3 x 2 £ 15, или x 2 £ 5, определяет полуплоскость, лежащую ниже прямой х 2 = 5.
Неравенство 3 x 1 £ 18, или x 1 £ 6, определяет полуплоскость, лежащую слева от прямой х 1 = 6.
О полуплоскостях x 1³ 0, x 2³ 0 подробно было сказано при решении примера 3 п. 5.5.3.
Область допустимых решений представляет многоугольник OABCDE.
Построим вектор N = (7;5).
Будем перемещать прямую, перпендикулярную вектору 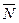 , в направлении этого вектора параллельно самой себе. Тогда точкой выхода из области будет точка С (5;3), являющаяся точкой пересечения прямых 2 x 1 + х 2 =13, 2 x 1 + З х 2 =19, и поэтому находится из системы уравнений этих прямых:
, в направлении этого вектора параллельно самой себе. Тогда точкой выхода из области будет точка С (5;3), являющаяся точкой пересечения прямых 2 x 1 + х 2 =13, 2 x 1 + З х 2 =19, и поэтому находится из системы уравнений этих прямых:
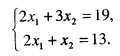
Отсюда:
3 х 1 – х 2 = 19 – 13; х 2 = 3,
2 х 1 = 19 – 3 х 2 = 19 – 9 = 10; х 1 = 5.
Следовательно, наибольшее значение целевой функции (5.32) достигается при x 1 = 5 х 2 = 3. Это значение равно:
F max = F (5;3) = 7×5 + 5×3 = 50.
Таким образом, мы видим, что для наиболее рационального использования сырья, гарантирующего предприятию наибольший доход, следует выпускать 5 единиц продукции вида Р 1 и 3 единицы вида Р 2, причем максимальный доход составит 50 денежных единиц. При этом сырье видов S 1 и S 2используется полностью, a S 3 и S 4 - не полностью, так как при плане выпуска продукции х 1 = 5, х 2 = 3:
2 х 1 + 3 х 2 = 5×2 + 3×3 = 19,
2 х 1 + х 2 = 5×2 + 3 = 13,
3 х 2 = 3×3 = 9 < 15,
3 х 1 = 3×5 = 15 < 18.
Задачи линейного программирования.
Графический метод.
Несмотря на то, что графический метод решения задач линейного программирования применяется только для задач с двумя искомыми переменными (или в случае трехмерного пространства с тремя), этот метод позволяет понять основную суть линейного программирования
Задача 1.
Рассмотрим систему неравенств
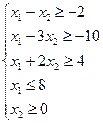 (1)
(1)
и линейную форму 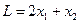 (2)
(2)
Найти минимум и максимум линейной формы (2) из области решений системы (1).
Решение.
Построим выпуклый многоугольник, заданный системой неравенств (1). Для этого построим прямоугольную систему координат х1ох2. Если в этой системе координат построить прямую ах1+bх2=с, то эта прямая разбивает плоскость х1ох2 на две полуплоскости, каждая из которых лежит по одну сторону от прямой. Сама прямая в этом случае называется граничной и принадлежит обеим полуплоскостям. Координаты точек, лежащих в одной полуплоскости удовлетворяют неравенству ах1+вх2≤с, а координаты точек, лежащих в другой полуплоскости, удовлетворяют неравенству ах1+вх2≥с. Построим в плоскости х1ох2 граничные прямые:
1)  4)
4) 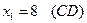
2) 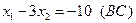 5)
5) 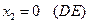
3) 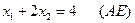
В результате получим пятиугольник АВСDЕ (рис. 2)
Значения х1 и х 2, удовлетворяющие системе неравенств (1), являются координатами точек, лежащих внутри или на границе найденного пятиугольника.
Теперь задача сводится к тому, чтобы найти те значения х 1 и х 2 при которых линейная форма L (2) имеет минимум, и те значения х1 и х 2 при которых линейная форма L достигает максимума. Из рис. 2 видно, что координаты всех точек, лежащих внутри или на границе пятиугольника, не являются отрицательными, т.е. все значения х 1 и х 2 больше или равны нулю.
Для каждой точки плоскости х1ох 2 линейная форма L принимает фиксированное значение. Множество точек, при которых линейная форма L принимает фиксированное значение L 1, есть прямая 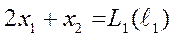 , которая перпендикулярна вектору
, которая перпендикулярна вектору 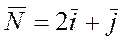 . Если прямую
. Если прямую 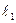 передвигать параллельно самой себе в положительном направлении вектора
передвигать параллельно самой себе в положительном направлении вектора 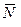 , то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую
, то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую 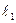 для того случая, когда L = 0, т.е. построим прямую
для того случая, когда L = 0, т.е. построим прямую  . Как видно из рис. 2, при передвижении прямой
. Как видно из рис. 2, при передвижении прямой 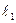 в положительном направлении вектора
в положительном направлении вектора 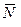 она впервые встречается с вершиной А(0;2) построенного пятиугольника АВСDЕ. В этой вершине линейная форма L имеет минимум. Следовательно,
она впервые встречается с вершиной А(0;2) построенного пятиугольника АВСDЕ. В этой вершине линейная форма L имеет минимум. Следовательно, 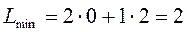 .
.
При дальнейшем передвижении прямой 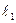 параллельно самой себе в положительном направлении вектора
параллельно самой себе в положительном направлении вектора 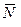 значение линейной формы будет возрастать, и оно достигает максимального значения в точке С(8;6). Таким образом,
значение линейной формы будет возрастать, и оно достигает максимального значения в точке С(8;6). Таким образом, 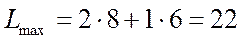 .
.
|

Задача 2.
Туристской фирме нужно не более 10 автобусов на 3 тонны и не более 8 автобусов на 5 тонн. Цена автобуса первой марки 20000 у.е., цена автобуса второй марки 40000 у.е.
Фирма может выделить для приобретения автобусов не более 400000 у.е. Сколько следует приобрести автобусов каждой марки в отдельности, чтобы их общая (суммарная) грузоподъёмность была максимальной.
Решение.
Пусть приобретено х 1 трёхтонных, х 2 пятитонных автобусов, тогда заданные условия задачи можно записать так:
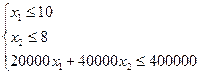 или
или 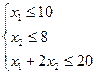 (1)
(1)
Линейная форма L (часто её называют целевой функцией) применительно к условиям нашей задачи имеет вид:
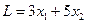 (2)
(2)
Требуется найти те значения х1 и х 2, при которых L достигает максимального значения. По условию задачи  . Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
. Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
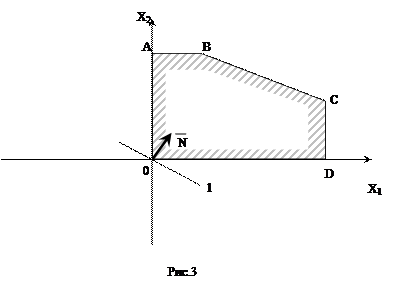
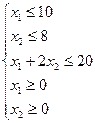 (3)
(3)
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1279; Нарушение авторских прав?; Мы поможем в написании вашей работы!