
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема. Решение уравнений колебания для полуограниченной струны
|
|
|
|
Л Е К Ц И И 6 - 8
с помощью формулы Даламбера. Решение уравнения колебаний методом разделения переменных. Решение неоднородного уравнения методом Фурье.
Рассмотрим задачу о распространении волн на полуограниченной прямой ( ). Эта задача имеет особенно важное значение при изучении процессов отражении волн от конца и ставится следующим образом.
). Эта задача имеет особенно важное значение при изучении процессов отражении волн от конца и ставится следующим образом.
Найти решение уравнения колебаний
 при
при 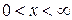 ,
, 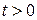 , (1)
, (1)
удовлетворяющее граничному условию
 (или
(или  )
) 
и начальным условиям
 (
( ). (2)
). (2)
Рассмотрим сначала случай однородного граничного условия
 (или
(или  )
)  (3)
(3)
то есть задачу о распространении начального возмущения на струне с закрепленным концом  .
.
Отметим следующие две леммы о свойствах решений уравнений колебаний, определенных на бесконечной прямой.
1. Если начальные данные в задаче о распространении колебаний на неограниченной прямой являются нечетными функциями относительно некоторой точки  , то соответствующее решение в этой точке
, то соответствующее решение в этой точке  равно нулю.
равно нулю.
2. Если начальные данные в задаче о распространении колебаний на не ограниченной прямой являются четными функциями относительно некоторой точки  , то производная по x соответствующего решения в этой точке равно нулю.
, то производная по x соответствующего решения в этой точке равно нулю.
Докажем лемму 1. Примем  за начало координат,
за начало координат,  = 0. В этом случае условия нечетности начальных данных запишутся в виде
= 0. В этом случае условия нечетности начальных данных запишутся в виде
 ,
,  .
.
Функция  , определяемая формулой Даламбера, при
, определяемая формулой Даламбера, при  и
и 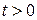 равна
равна
 ,
,
так как первое слагаемое равно нулю в силу нечетности  , а второе равно нулю, поскольку интеграл от нечетной функции в пределах, симметричных относительно начала координат, всегда равен нулю.
, а второе равно нулю, поскольку интеграл от нечетной функции в пределах, симметричных относительно начала координат, всегда равен нулю.
Аналогично доказывается лемма 2. Условия четности начальных данных имеет вид
 ,
,  .
.
Заметим, что производная четной функции является функцией нечетной
 .
.
Из формулы Даламбера следует
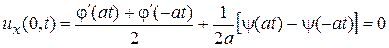 ,
, 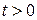 ,
,
так как первое слагаемое равно нулю в силу нечетности 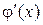 , а второе – в силу четности
, а второе – в силу четности 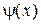 .
.
Для решения нашей задачи (1)-(3), рассмотрим функции  и
и 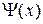 , являющиеся нечетным продолжением
, являющиеся нечетным продолжением  и
и 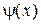 , входящих в условие (2):
, входящих в условие (2):


Функция

определена для всех x и 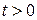 . В силу леммы 1
. В силу леммы 1
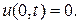
Кроме того, эта функция удовлетворяет при  и
и  следующим начальным условиям:
следующим начальным условиям:

 .
.
Таким образом, рассматривая полученную функцию 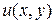 только для
только для  ,
,  , мы получим функцию, удовлетворяющую всем условиям поставленной задачи.
, мы получим функцию, удовлетворяющую всем условиям поставленной задачи.
Возвращаясь к прежним функциям, можно написать:
 (4)
(4)
В области 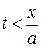 , для бесконечной прямой, влияние граничных условий не сказывается. Выражение для
, для бесконечной прямой, влияние граничных условий не сказывается. Выражение для  в этом случае совпадает с решением Даламбера.
в этом случае совпадает с решением Даламбера.
Аналогично, если при  мы имеем свободный конец
мы имеем свободный конец

то, для четного продолжения функций  и
и 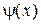
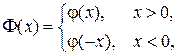

получим решение уравнения колебаний
 ,
,
или
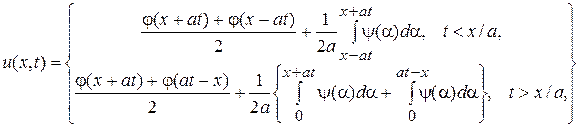 ,
,
удовлетворяющее в области  начальным условиям (2) и граничному условию
начальным условиям (2) и граничному условию  .
.
Решение уравнения колебаний методом разделения переменных
Метод разделения переменных, или метод Фурье является одним из наиболее распространенных методов решения уравнений с частными производными.
Будем искать решение уравнения
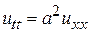 (1)
(1)
удовлетворяющее однородным граничным условиям
 ,
,  (2)
(2)
и начальным условиям
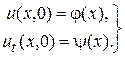 (3)
(3)
Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Будем искать частное решение уравнения (1) в виде:
 , (4)
, (4)
где 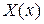 - функция только переменного x,
- функция только переменного x,  - функция только переменного t.
- функция только переменного t.
Подставляя предполагаемую форму решения (4) в уравнение (1), получим:

или, после деления на XT,
 , (5)
, (5)
где l - постоянная. Из соотношения (5) получаем обыкновенные дифференциальные уравнения для определений функций 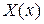 и
и 

 , (6)
, (6)

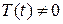 . (7)
. (7)
Граничные условия (2) дают:


Отсюда следует, что функция 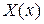 должна удовлетворять дополнительным условиям
должна удовлетворять дополнительным условиям
 .
.
Таким образом, мы приходим к простейшей задаче: найти значения параметра l, при которых существуют нетривиальные решения задачи:
 (8)
(8)
а также найти эти решения. Такие значения параметра l называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (8).
Рассмотрим отдельно случаи, когда параметр l отрицателен, равен нулю или положителен.
1. При l < 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнение (6) имеет вид:
 .
.
Граничные условия дают:
 ,
,
 (
( ),
),
то есть
 и
и  .
.
Но в рассматриваемом случае a - действительно и положительно, так что  . Поэтому
. Поэтому  ,
, 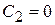 и, следовательно,
и, следовательно,  .
.
2. При  также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (6) имеет вид:
также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (6) имеет вид:
 .
.
Граничные условия дают:
 ,
,  ,
,
то есть,  и
и 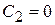 и, следовательно,
и, следовательно,  .
.
3. При  общее решение уравнения (6) может быть записано в виде:
общее решение уравнения (6) может быть записано в виде:
 .
.
Граничные условия дают:

 .
.
Если 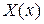 не равно тождественно нулю, то
не равно тождественно нулю, то  , поэтому
, поэтому
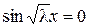
откуда
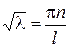 ,
,
где n - любое целое число. Следовательно, нетривиальные решения задачи (8) возможны лишь при значениях
 . (9)
. (9)
Этим собственным значениям соответствуют собственные функции
 ,
,
где  - произвольная постоянная.
- произвольная постоянная.
Итак, только при значениях l, равных  , существуют нетривиальные решения задачи (8)
, существуют нетривиальные решения задачи (8)
 , (10)
, (10)
определяемые с точностью до произвольного множителя, который мы положили равным единице. Этим же значениям  соответствуют решения уравнения (7)
соответствуют решения уравнения (7)
 , (11)
, (11)
где 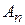 и
и  - произвольные постоянные.
- произвольные постоянные.
Возвращаясь к задаче (1) - (3), заключаем, что функции

являются частными решениями уравнения(1), удовлетворяющими граничным условиям (2) и представимыми в виде произведения (4) двух функций, одна из которых зависит только от x, другая – от t. В силу линейности и однородности уравнения (1) сумма частных решений
 (12)
(12)
также удовлетворяет этому уравнению и граничным условиям (2). Начальные условия позволяют определить 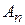 и
и  . Потребуем, чтобы функция (12) удовлетворяла условиям (3):
. Потребуем, чтобы функция (12) удовлетворяла условиям (3):
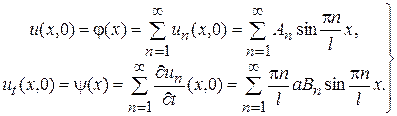 (13)
(13)
Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция 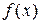 , заданная в промежутке
, заданная в промежутке  , разлагается в ряд Фурье:
, разлагается в ряд Фурье:
 ,
,
где
 .
.
Если функции  и
и 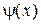 удовлетворяют условиям разложения в ряд Фурье, то
удовлетворяют условиям разложения в ряд Фурье, то
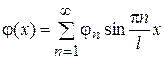 ,
,  ,
,
 ,
, 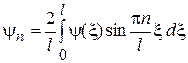 .
.
Сравнение этих рядов с формулами (13) показывает, что для выполнения начальных условий надо положить
 ,
, 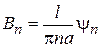 ,
,
чем полностью определяется функция (12), дающая решение исследуемой задачи.
Интерпретация решения. Функцию  можно представить в виде
можно представить в виде

 ,
,
где
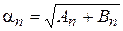 ,
,  .
.
Каждая точка струны  совершает гармонические колебания
совершает гармонические колебания

с амплитудой
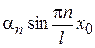 .
.
Движение струны такого типа называется стоячей волной. Точки  , в которых
, в которых  , в течение всего процесса остаются неподвижными и называются узлами стоячей волны. Точки
, в течение всего процесса остаются неподвижными и называются узлами стоячей волны. Точки  , в которых
, в которых  , совершают колебания с максимальной амплитудой
, совершают колебания с максимальной амплитудой 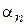 .
.
Профиль стоячей волны в любой момент времени представляет синусоиду
 ,
,
где

 .
.
В момент времени t, при котором  , отклонения достигают максимальных значений, а скорость движения равна нулю. В момент времени t, при которых
, отклонения достигают максимальных значений, а скорость движения равна нулю. В момент времени t, при которых 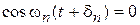 , отклонение равно нулю, а скорость движения максимальна. Частоты
, отклонение равно нулю, а скорость движения максимальна. Частоты 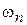 - называются собственными частотами колебаний струны.
- называются собственными частотами колебаний струны.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 2043; Нарушение авторских прав?; Мы поможем в написании вашей работы!