Решение неоднородного уравнения методом Фурье

Рассмотрим неоднородное уравнение колебаний

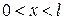, (1)

с начальными условиями

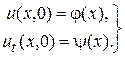
(2)

и однородными граничными условиями

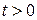, , . (3)

Вынужденные колебания общего типа, можно представить как результат сложения двух колебательных движений. Одно из них есть чисто вынужденное колебание, то есть, такое, которое совершается под действием силы 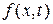, причем струна в начальный момент не выведена из состояния покоя, другое есть свободное колебание, которое струна совершает без действия силы, только вследствие начального возмущения. Аналитически это приводит к введению вместо u двух новых функции v и w, по формуле

,

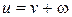где функция v удовлетворяет условиям

, (4)

и , ,

и дает чисто вынужденное колебание, а функция w удовлетворяет условиям

, (5)

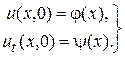и , .

и дает свободное колебание. Методы нахождения свободных колебаний w были указаны в ранее, так что здесь мы остановимся только на нахождении функции v. Как и в случае свободных колебаний, будем искать решение задачи (4) в виде разложения в ряд Фурье по x

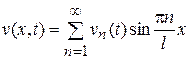, (6)

рассматривая при этом t как параметр. Для нахождения 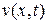надо определить функцию . Представим функцию 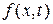ряда Фурье:

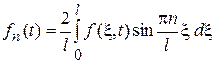, (7)

Подставляя предполагаемую форму решения (6) в исходное уравнение (4)

,

видим, что оно будет удовлетворено, если все коэффициенты разложения равны нулю, то есть,

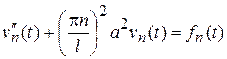. (8)

Для определения мы получили обыкновенное дифференциальное уравнение с постоянными коэффициентами. Для удовлетворения начальным условиям достаточно подчинить функции этим условиям, т.е. положить

, , (9)

Решение уравнения (8) с дополнительными условиями (9) есть:

, (10)

Подставив выражение (10) в (6), мы и получим выражение для .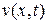

Таким образом, искомое решение задачи запишется в виде

.

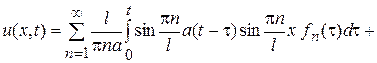
Вторая сумма представляет собой решение задачи о свободных колебаниях струны, при заданных начальных условиях, и была исследована выше.

Дата добавления: 2014-01-13