Показатели работы отраслей

Модель Леонтьева многоотраслевой экономики

Лекция 6. Линейные экономические модели

Эффективное ведение народного хозяйства предполагает наличие баланса между отдельными отраслями.

Предположим, что вся производящая сфера народного хозяйства разбита на некоторое число n отраслей, каждая из которых производит свой продукт

Производственное потребление	Конечное потребление	Валовой выпуск

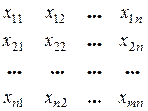
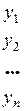
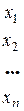
Балансовый характер этой таблицы выражается в том, что при любом i = l,..., n должно выполняться соотношение

x_i = x_{i 1} + x_{i 2} +...+ x_in + y _i, (1)

означающее, что валовой выпуск x_i расходуется на производственное потребление, равное x _i1 + x_{i 2} +...+ x_in, и непроизводственное потребление, равное у_i. Будем называть (14) соотношениями баланса.

Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки, киловатт-часы и т.п.), или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевой балансы. Для определенности в дальнейшем будем иметь в виду (если не оговорено противное) стоимостной баланс.

В. Леонтьев, рассматривая развитие американской экономики в предвоенный период, обратил внимание на важное обстоятельство. А именно, величины 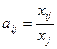остаются постоянными в течение ряда лет. Это обуславливается примерным постоянством используемой технологии.

В соответствии со сказанным сделаем такое допущение: для выпуска любого объема х_j продукции отрасли j необходимо затратить продукцию отрасли i в качестве a_ij x _j, где а_ij – постоянный коэффициент. Проще говоря, материальные издержки пропорциональны объему производимой продукции. Это допущение постулирует, как говорят, линейность существующей технологии. Принцип линейности распространяется и на другие виды на оплату труда, а также на нормативную прибыль. Итак, согласно гипотезе линейности имеем

x_ij = a_ij x_j (i, j =1,..., n). (2)

Коэффициенты а_ij называют коэффициентами прямых затрат (коэффициент материалоемкости).

В предположении линейности соотношения (2) принимают вид:

x ₁ = a ₁₁ x ₁ + a ₁₂ x ₂ + … + a _{1 n} x_n + y ₁

x ₂ = a ₂₁ x ₁ + a ₂₂ x ₂ + … + a _{2 n} x_n + y ₂

…………………………………..

x_n = a_{n 1} x ₁ + a_{n 2} x ₂ + … + a_nn x_n + y_n,

или, в матричной записи,

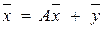, (3)

где

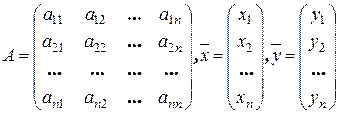
Вектор 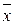называется вектором валового выпуска, вектор 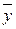– вектором конечного потребления, а матрица А – матрицей прямых затрат. Соотношение (3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов 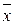и 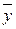это соотношение называют также моделью Леонтьева.

Уравнения межотраслевого баланса можно использовать для целей планирования. В этом случае задача ставится так: для предстоящего планового периода [ T ₀, T ₁] задается вектор 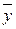конечного потребления. Требуется определить вектор 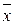валового выпуска. Проще говоря, нужно решить задачу: сколько следует произвести продукции различных видов, чтобы обеспечить заданный уровень конечного потребления? В этом случае необходимо решить систему линейных уравнений (3) с неизвестным вектором 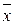при заданных матрице А и вектору 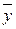. При этом нужно иметь в виду следующие особенности системы (3):

1. Все компоненты матрицы А и вектора 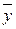неотрицательны (это вытекает из экономического смысла А и 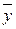). Для краткости будем говорить о неотрицательности самой матрицы А и вектора 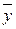и записывать это так: .

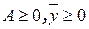2. Все компоненты вектора 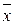также должны быть неотрицательными: .

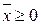Замечание. Обратим внимание на смысл коэффициентов а_ij прямых затрат в случае стоимостного (а не натурального) баланса. В этом случае из (16) видно, что a_ij совпадает со значением х_ij при x_j = 1 (1 руб.).

Таким образом, а_ij есть стоимость продукции отрасли i, вложенной в 1 руб. продукции отрасли j. Отсюда, между прочим, видно, что стоимостной подход по сравнению с натуральным обладает более широкими возможностями, при таком подходе уже необязательно рассматривать «чистые», т. е. однопродуктовые, отрасли. Ведь и в случае многопродуктовых отраслей тоже можно говорить о стоимостном вкладе одной отрасли в выпуск 1 руб. продукции другой отрасли; скажем, о вкладе промышленной сферы в выпуск 1 руб. сельскохозяйственной продукции или о вкладе промышленной группы А (производство предметов потребления). Вместе с тем надо понимать, что планирование исключительно в стоимостных величинах может легко привести к дисбалансу потоков материально-технического снабжения.

Пример 1. Таблица содержит данные баланса трех отраслей промышленности за некоторый период времени. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить, соответственно, до 60, 70и 30 условных денежных единиц.

Решение. Выпишем векторы валового выпуска и конечного потребления и матрицу коэффициентов прямых затрат. Согласно формуле (3), имеем:

, , .

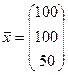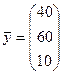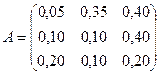Матрица А удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь вид

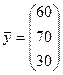. (4)

Требуется найти новый вектор валового выпуска 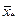, удовлетворяющий соотношениям баланса в предположении, что матрица А не изменяется. В таком случае компоненты 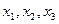неизвестного вектора 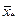находятся из системы уравнений, которая в матричной форме имеет следующий вид:

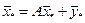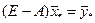, или . (5)

Матрица этой системы

.

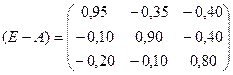Решение системы линейных уравнений (9.3) при заданном векторе пвой части (9.12) (например, методом Гаусса) дает новый вектор 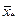как решение уравнений межотраслевого баланса:

.

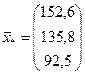Таким образом, для того чтобы обеспечить заданное увеличение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и переработку углеводородов на 52,2 %, уровень энергетики – на 35,8 % и выпуск машиностроения – на 85 % – по сравнению с исходными величинами, указанными в табл. 10.

Дата добавления: 2014-01-13