Продуктивные модели Леонтьева

Определение. Матрица А ³ 0 называется продуктивной, если для любого вектора 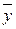³ 0 существует решение 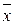³ 0 уравнения (9.1)

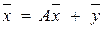(5)

В этом случае модель Леонтьева, определяемая матрицей А, тоже называется продуктивной.

Итак, модель Леонтьева продуктивна, если любой вектор 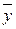³0конечного потребления можно получить при валовом выпуске 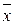³0.

Нижеследующая теорема 1 показывает, что нет необходимости требовать существования решения 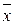³0 уравнения (9.1) для любого вектора 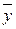³0. Достаточно, чтобы такое решение существовало хотя бы для одного вектора 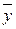³ 0.

Условимся в дальнейшем писать 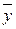³0 и называть вектор 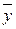положительным, если все компоненты этого вектора строго положительны.

Теорема 1 (первый критерий продуктивности.) Если А ³0 и для некоторого положительного вектора 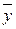^* уравнение (7.3) имеет решение 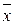^* ³ 0, то матрица А продуктивна.

Заметим, что на самом деле 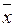> 0, что следует из 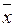^*= А 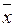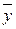^* + ^* и А 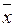³ 0, 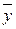^*³ 0, ^* ³0.

Уравнение Леонтьева (9.1) можно записать следующим образом:

(Е - А) 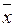= 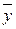, (6)

где Е - единичная матрица.

Возникает, естественно, вопрос об обращении матрицы Е - А.

Понятно, что если обратная матрица (Е - А) ^-1существует, то из (6) вытекает

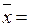(Е - А)^-1 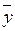(7)

Следующая теорема дает более эффективное условие продуктивности, чем теорема 1

Теорема 2 (второй критерий продуктивности). Матрица А ³ 0 продуктивна тогда и только тогда, когда матрица (Е – А)^-1 существует и неотрицательна.

Доказательство. Если (Е – А)^-1 существует и ³ 0, то из формулы (7) следует продуктивность матрицы А.

Обратно, пусть матрица А продуктивна, Рассмотрим следующие системы уравнений:

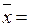
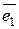(Е – А) , (Е – А) ,..., (Е – А) 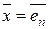, где е ₁, е₂,…, е_n – столбцы единичной матрицы. Каждая из этих систем в силу продуктивности матрицы А имеет неотрицательное решение, т.е. существуют такие векторы (столбцы) 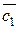³ 0, 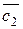³ 0,..., 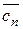³ 0, что

(Е – А) 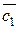= 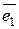, (Е – А)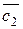= 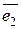,..., (Е – А) 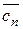= 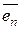. (9.6)

Обозначим через С матрицу, составленную из столбцов с ₁, с₂, ..., с_п. Тогда вместо п равенств (9.6) можно написать одно: (Е – А) С = Е.

Следовательно, матрица (Е – А)имеет обратную С, причем С ³ 0. Теорема доказана.

Пример 1. Исследуем на продуктивность матрицы

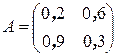
В данном случае

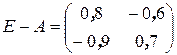
Необходимые вычисления предоставим читателю провести самостоятельно. Получаем матрицу (Е – А)^-1, которая существует и равна

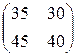
Мы видим, что эта матрица неотрицательна. Следовательно, А продуктивна.

Теорема 3. (третий критерий продуктивности). Матрица А ³0 продуктивна тогда и только тогда, когда сходиться бесконечный ряд.

Е + А + А ² +... (8)

Полученный нами критерий продуктивности матрицы А (сходимость ряда (8)) в ряде случаев может быть использован для проверки матрицы А на продуктивность. Покажем, например, что если сумма элементов любого столбца неотрицательной матрицы А меньше 1^*, то А продуктивна. Действительно, пусть q - наибольшая из указанных сумм, q <1. Ясно, что тогда все элементы матрицы А не превосходят q. Из правила перемножения матриц легко вывести, что любой элемент матрицы А ² не превосходит q ²:

( A ²)_ij = a_{i 1} a _jl + a_{i 2} a_{j 2} +...+ a_ina_nj £ q (a_{i 1} +...+ a_nj) < q ² <1.

Точно так же получим, что элементы матрицы А ³ не превосходит q ³ и т.д. Отсюда следует сходимость ряда (8), а значит, и продуктивность матрицы А.

Напримердля матрицы

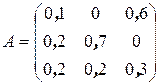
сумма элементов каждого столбца меньше единицы. Следовательно, А продуктивна.

Аналогично доказывается, что если в неотрицательной матрице А сумма элементов любой строки меньше 1, то матрица А продуктивна. Впрочем, то же самое можно вывести и из следующего предложения: если продуктивна матрица А, то продуктивна и матрица А ^т,что следует из теоремы 2.

Пусть А 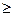0 – продуктивная матрица. Запасом продуктивности матрицы А назовем такое число 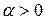, что все матрицы 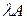, где 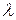1<<1 + 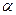, продуктивны, а матрица (1 +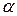) А – не продуктивна.

Пример 2. Выяснить, какой запас продуктивности имеет матрица А из примера 30.

Решение. Будем руководствоваться критерием продуктивности из теоремы 2 (существование неотрицательной матрицы (Е – А)^-1). В данном случае

Определитель этой матрицы

.

Обратной матрицей будет

.

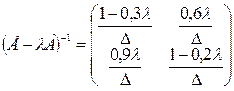Для продуктивности 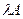нужно, чтобы все элементы обратной матрицы были неотрицательны, т.е. 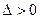, , 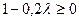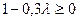. Имеем 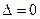при , 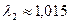. Отсюда матрица 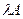продуктивной при 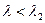, т.е. 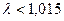. Запас продуктивности матрицы А равен 0,015.

Задания для самостоятельной работы

Задача 1. Отрасль состоит из четырех предприятий: вектор выпуска продукции и матрица коэффициентов прямых затрат имеют вид

, .

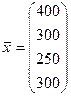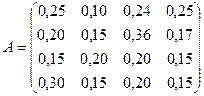Найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.

Задача 2. Предприятие выпускает три вида продукции с использованием трех видов сырья, характеристики производства указаны в табл. 9.3.

Таблица 9.3

Дата добавления: 2014-01-13