Звідси маємо

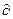
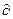b^’_i / b_k,= b^’_ik, i = 1, m, k = 1, m.

Таким чином, зміна запасу k-го ресурсу на величину b_k призводить до зміни правої частини i-го рівняння оптимальної симплекс-таблиці на величину

b_i = b^’_ik b_k. Граничне значення b_k визначається умовою невід’ємності усіх правих частин b^’_i після зміни запасу k-го ресурсу. Тому множина допустимих значень b_k. Визначається як розв’язок системи

b^’_i + b^’_ik b_k ³ 0, i = 1, m. (8.4)

Для розв’язування системи (8.4) треба знати усі b^’_ik. Виявляється, що ця інформація міститься у оптимальній симплекс-таблиці. Дійсно, результатом множення матриці B^-1~ на одиничний стовпець з одиницею у i-му рядку є i–й стовпець матриці B^-1~. Тому, якщо a^j - базисний стовпець матриці A, який містить одиницю у i-му рядку, то стовпець оптимальної симплекс-таблиці a^j’ - i–й стовпець матриці B^-1~.

У випадку, коли додаткова змінна, відповідаюча k-му ресурсу, у оптимальній симплекс-таблиці базисна, k-й стовпець матриці B^-1~ одиничний, і тому система (8.4) вироджується у одну нерівність b_k ³ -b^’_i.

Для прикладу, розглянутого у лекції 6 (табл.6.2), ресурсам відповідають такі системи нерівностей:

першому –

10/3 + 5/6b₁ ³ 0,

4/3 - 2/3b₁ ³ 0,

10/3 + 17/6b₁ ³ 0;

другому -

10/3 - 1/6b₂ ³ 0,

4/3 + 1/3b₂ ³ 0,

10/3 - 13/6b₂ ³ 0;

третьому –

b₃ ³ -10/3.

Розв’язавши ці системи, отримуємо

-20/17 £ b₁ £ 2, b_1min = 8 – 20/17 = 116/17, b_1max = 8 + 2 = 10;

-4 £ b₂ £ 20/13, b_2min = 20 – 4 = 16, b_2max = 20 + 20/13 = 280/13;

-10/3 £ b₃ <, b_3min = 24 – 10/3 = 62/3.

Отримані максимальні запаси дефіцитних ресурсів і мінімальний запас недефіцитного ресурсу співпадають з визначеними графічним методом.

Визначення інтервалів для коефіцієнтів цільової функції

Розглянемо визначення діапазонів значень коефіцієнтів цільової функції, зберігаючих незмінним статус ресурсів у оптимальній симплекс-таблиці. Нехай, у початковій симплекс-таблиці, для якої отримано розв’язок симплекс-методом, коефіцієнт c_j отримує приріст c_j. Тоді після виконання тих самих перетворень таблиць, що і при початковому значенні c_j, отримуємо таблицю, що відрізняється від отриманої раніше оптимальної симплекс-таблиці значенням c^’_j, що зростає на c_j. Умовою допустимих значень c_j. є можливість переходу від отриманої таблиці до оптимальної симплекс-таблиці при фіксованому базисі шляхом додавання до одних рядків інших, помножених на деякі коефіцієнти.

Якщо змінна x_j у отриманій таблиці базисна, то у шуканій оптимальній симплекс-таблиці коефіцієнт c^’_j індексного рядка повинен бути нульовим. Досягти цього можна шляхом множення рядка, якому відповідає базисна змінна x_j, на c^’_j і віднімання отриманого добутку від індексного рядка. Результатом буде рядок з нульовим коефіцієнтом при x_j та зміненими іншими коефіцієнтами. Умовою допустимого значення c_j є недодатність усіх коефіцієнтів нового індексного рядка при пошуку максимуму цільової функції або невід’ємність – при пошуку мінімуму. Останню умову треба перевіряти тільки для небазисних стовпців, оскільки у базисних стовпцях у індексному рядку зберігаються нульові значення. Таким чином діапазон допустимих значень c_j для базисної змінної x_j, що відповідає i-му рядку, визначається з системи

c^’_k - a^’_ik c_j £ 0, k N

у випадку пошуку максимуму, і з системи

c^’_k - a^’_ik c_j ³ 0, k N

при пошуку мінімуму,

де N – множина індексів небазисних змінних отриманої симплекс-таблиці.

Якщо змінна x_j – небазисна, діапазон допустимих значень c_j при пошуку максимуму (мінімуму) визначається з умови недодатності (невід’ємності) нового значення c^’_j, тобто з нерівності c^’_j + c_kj £ 0 (c^’_j + c_kj ³ 0).

У прикладі, розглянутому у попередній лекції (табл.6.2), обидві змінні x₁ і x₂ базисні. Для c₁ і c₂ відповідно отримуємо системи

-5/2 – 5/6c₁ £ 0,

-1/2 + 1/6c₁ £ 0;

-5/2 + 2/3c₂ £ 0,

-1/2 – 1/3c₂ £ 0.

Розв’язок цих систем має вигляд

-3 £ c₁ £ 3, c_1min = 7 – 3 = 4, c_1max = 7 + 3 = 10;

-3/2 £ c₂ £ 15/4, c_2min = 5 – 3/2 = 7/2, c_2max = 5 + 15/4 = 35/4.

Дата добавления: 2014-01-13