Булевы функции. Табличное задание функции

Табличное задание функции

Как и бинарный закон компо­зиции, однородная функция двух переменных может быть задана таблицей соответствия (матрицей), строки и столбцы кото­рой соответствуют буквам алфавита. Таким способом можно представлять функции одной и двух переменных. Для представления функций трех и большего числа переменных потребовались бы трехмерные и, вообще, п -мерные таблицы. Этого можно избежать, если столбцы матрицы поставить в соответствие не буквам алфавита, а словам, т.е. образовать k столбцов. Для каждой функции отводится строка, клетки которой запол­няются буквами из данного алфавита. Матрицавсех функций п переменных в k -значном алфавите содержит 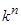строк и называ­ется общей таблицей соответствия. Например, для k =3 и п = 2 такая матрица имеет вид:

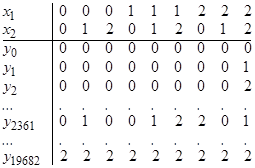
Номера столбцов определяются расположенными над ними п -разрядными числами с основанием k, каждое из которых чита­ется сверху вниз. Номера функций отождествляются с 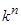-разрядными числами, которые соответствуют строкам матрицы в той же системе счисления.

Наиболее простым и в то же время важнейшим классом однородных функций являются двузначные (булевы) функции.

Областью определения булевых функций от п переменных слу­жит множество слов длины п. Они представляют собой всевозмож­ные наборы из п двоичных цифр и их общее количество равно .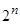

Число всевозможных булевых функций п переменных 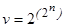быстро возрастает с увеличением п (при п = 3 оно равно 256, а при п = 5 превышает 4 миллиарда). Но функции одной и двух перемен­ных еще можно перечислить и подробно исследовать, так как их количество сравнительно невелико (v = 4 при п = 1 и v = 16 при п = 2).

Общаятаблица соответ­ствия для булевых функций одной переменной имеет следующий вид (справа указаны обозначения функций):

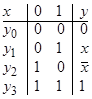
Две функци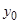и = 0 и = 1 представляют собой функции-константы (тождественный ноль и тождественная единица), так как они не изменяют своих значений при изменении аргумента. Функ­ция = х повторяет значения переменной х и потому просто сов­падает с ней.

Единственной нетривиальной функцией является 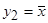, назы­ваемая отрицанием или инверсией. Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.

Все 16 функций двух переменных приведены в табл. 9.1, где указаны условные обозначе­ния, названия и значения функции (в скобках даны встречающиеся в литературе варианты).

Шесть из приведенных функций не зависят от x ₁ или x ₂ (или от обоих вместе). Это две константы (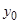= 0 и = 1), повторения (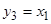и 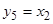) и отрицания (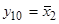и 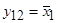), являющиеся функциями одной переменной (x ₁ или x ₂). Из остальных десяти функ­ций две (и 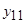) отличаются от соответствующих и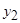м (и ) лишь порядком расположения аргументов и поэтому не являются само­стоятельными. Поэтому из 16 булевых функций двух переменных только восемь являются оригинальными ().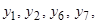

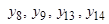Таблица 9.1

Дата добавления: 2014-01-13