Основные определения. Вопрос 5. Взаимное расположение точки и плоскости

Логические функции

Вопрос 5. Взаимное расположение точки и плоскости

Точка может лежать в плоскости или быть вне ее.

Если точка лежит в плоскости общего положения, то ее проекции должны лежать на проекциях какой-либо прямой, принадлежащей данной плоскости.

Итак, если точка лежит на вспомогательной прямой, принадлежащей плоскости, то она лежит в этой плоскости.

Пусть имеется функция, заданная на некотором множестве М. Функция называется логической, если она принимает значения в конечном множестве N. Если множество N содержит п элементов, то логическая функция называется п -значной. Перечень всех символов, соответствующих области значений логической функции, называется алфавитом, а сами элементы множества N – буквами этого алфавита.

Логическая функция называется однородной, если её аргументы принадлежат тому же множеству, что и значение функции. Другими словами, логическая функция отображает декартову степень множества N ⁿ в само множество N. Областью определения однородной функции 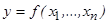служит множество наборов 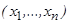, называемых словами, где каждый из аргументов замещается буквами k -ичного алфавита {0, 1, …, k -1}. Количество п букв в данном слове определяет его длину.

Определим общее число различных однородных логических функций n переменных. Очевидно, число всевозможных слов длины п в k -ичном алфавите равно 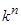. Так как каждому из этих слов можно поставить в соответствие любое из k значений множества N, то общее количество однородных логических функций n переменных равно .

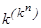Если буквами алфавита служат числа от 0 до k- 1, то каждое слово 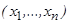символически представляется упорядоченной последовательностью п таких чисел и рассматривается как запись п -разрядного числа в позиционной системе счисления с основанием k, т. е. 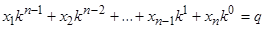. Числа 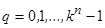служат номерами слов и тем самым на множестве всех слов вводится естественная упорядоченность (отношение стро­гого порядка). Аналогично номерами функций можно считать 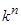-разрядные числа в той же системе счисления.

Так, в трехзначном алфа­вите {0, 1, 2} словами длины 4 будут все четырехразрядные числа с основанием k = 3, т. е. 0000, 0001, 0002, 0010, 0011,..., 2221, 2222, которые соответствуют десятичным числам от 0 до 80. Поставив каждому такому четырехразрядному числу в соответствие одну из букв алфавита {0, 1, 2}, получим некоторую функцию четырех переменных,причем количество таких функций выражается огромным числом 3⁸¹.

Дата добавления: 2014-01-13