Лекция 6. Модель обучения навыкам алгоритмической природы (МОНАП)

Модель обучения навыкам алгоритмической природы (МОНАП)

В соответствии с теорией поэтапного формирования умственных действий процесс обучения представляет собой управляемый и контролируемый процесс выполнения учебных заданий обучаемым.

В каждом шаге обучения можно выделить следующие четыре этапа:

1) выдача учебного задания с требуемыми свойствами;

2) ввод ответа обучаемого, контроль правильности выполнения задания и выдача подкреплений, а в случае появления ошибок, выдача соответствующих объяснений;

3) идентификация знаний обучаемого и вынесение решения:

- о продолжении обучения,

- о достижении цели обучения,

- об аварийном окончании обучения (обучаемый отсылается к преподавателю или к соответствующей литературе);

4) определение необходимых данных для выдачи очередного задания (определение требуемых свойств задания) при вынесении решения о необходимости продолжения обучения.

Рассматриваемая модель обучения обеспечивает полную формализацию, а на ее основе и автоматизацию третьего и четвертого этапов шага обучения.

В соответствии с алгоритмическим подходом к организации процесса обучения задается алгоритмическое предписание Q. Алгоритмическое предписание разрабатывается экспертом-педагогом и описывает пути решения учебных задач из заданной предметной области (ПО) обучения.

Алгоритмическое предписание включает в себя совокупность элементарных операций и указывает требуемую (или желаемую) последовательность их выполнения, приводящую к правильному решению учебных задач.

Множество типов операций, выполняемых обучаемым при решении задач заданной ПО обучения и соответствующих алгоритмическому предписанию Q, обозначается через Y=[y ₁, y ₂,…,y_j,…,y_J].

Все задачи ПО обучения могут быть разделены на R классов, каждый из которых характеризуется соответствующим уникальным подмножеством типов операций Y_r Ì Y (U_r Y_r=Y; r=1,2,…R), используемым при выполнении задач, принадлежащих r-му классу.

В качестве основного компонента модели обучаемого, используется вектор:

P(k)=[P ₁ (k), P ₂ (k),…,P_j(k),…,P_J(k)] (2.1)

где: P_j(k) - вероятность правильного применения операции y_j на k-м шаге обучения (j = 1, 2,…, J).

Модель обучаемого служит для идентификации знаний обучаемого на каждом шаге обучения.

Аналогично принимаются следующие предположения:

§ уровень обученности, т.е. значение P_j(k) для всех j в течение выполнения задания на k-м шаге, остается постоянным;

§ отсутствует взаимодействие операций, т.е. значение 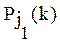не зависит от значения для любых j ₁, j ₂;

§ операция 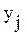независимо от того, в какой части задачи она выполняется, будет определяться тем же самым значением

P_j(k) для всех задач задания, которое может состоять из одной или нескольких задач.

Сложность задания S(k), выданного на k-м шаге обучения, определяется как:

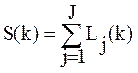(2.2)

где: 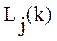- число операций 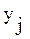, использование которых необходимо при выполнении задания.

Мера трудности задания T(k) вводится как средняя доля ошибок, ожидаемых при выполнении задания, т.е.:

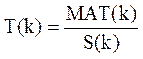(2.3)

где: MAT(k) - математическое ожидание числа ошибок при выполнении задания.

Так как число ошибок для каждого типа операций является дискретной случайной величиной, распределенной по биномиальному закону, и предполагается, что отсутствует взаимодействие операций, то для вычисления MAT(k) используется следующая формула:

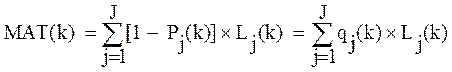(2.4)

где: q_j(k) - вероятность неправильного применения операции y_j на k-м шаге обучения.

В соответствии с ассоциативно-рефлекторной теорией усвоения необходимо стремиться к тому, чтобы на каждом шаге обучения выполнялось неравенство:

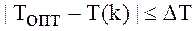(2.5)

где: 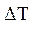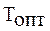- оптимальная мера трудности (обычно 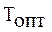= 0,5, т.е. задание должно быть средней, посильной для обучаемого, трудности);

- размер интервала.

В связи с тем, что операции 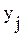, используемые при решении задач,

в общем случае связаны между собой определенными структурными и количественными отношениями, описываемыми алгоритмическим предписанием Q, и варьировать эти отношения можно только в определенных пределах, то не всегда удается обеспечить режим стабилизации такого параметра обучения, как мера трудности, то есть для некоторых k имеет место:

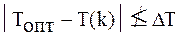(2.6)

Если для всех операций y_j имеет место одно из двух следующих неравенств:

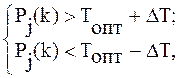(2.7)

указанная стабилизация T(k) невозможна.

В общем случае учебное задание может содержать несколько задач. Использование многозадачного задания целесообразно, когда входящие в него задачи отличаются друг от друга подмножествами типов операций, используемыми при их выполнении, так как в противном случае происходит лишь задержка обратной связи. Вводится понятие максимальной емкости задания 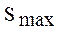, равной максимально возможному числу задач в формируемом задании.

Если число задач в задании меньше 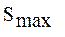и трудность задания стала меньше оптимальной, то добавлением новых задач в задание удается приблизить значение трудности задания к оптимальному (или достичь оптимального) за счет введения новых типов операций. При этом принцип перехода к усвоению нового учебного материала только в случае успешного усвоения предыдущего материала нарушается. В этом случае, как и в случае, когда стабилизация T(k) невозможна, управление обучением осуществляется не на оптимальном, а на ограниченно-оптимальном уровне.

С учетом введенных определений и предложений, используя подход, аналогичный предложенному в, формулируется цель обучения:

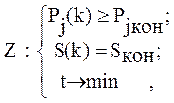(2.8)

где: 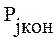- требуемое значение вероятности правильного применения операции;

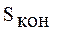- требуемая сложность задачи в r-м классе задач (r = 1,2,…,R);

t - время обучения.

Для определения 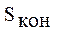используется формула:

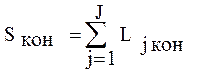(2.9)

где: 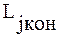- требуемое число операций 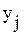в задаче с требуемой сложностью.

Целью обучения является достижение заданного уровня обученности в каждом классе задач ПО обучения при одновременной минимизации времени обучения t (экстремальная цель), где уровень обученности определяется следующим образом: оценка вероятности правильного применения операции 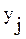при выполнении задачи требуемой сложности 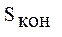должна удовлетворять неравенству:

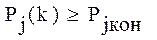(2.10)

Если достигнут заданный уровень обученности, то обучение заканчивается.

Если хотя бы в одном классе задач ПО обучения имеет место одно или оба из неравенств в следующей системе:

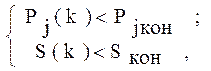(2.11)

то обучение продолжается.

На каждом шаге обучения, начиная с 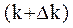-го 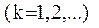производится проверка на аварийное окончание. Аварийное окончание обучения осуществляется, если хотя бы для одной операции имеет место система неравенств:

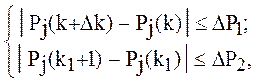(2.12)

где: 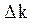- предаварийное (критическое) число шагов обучения, во время которых характеристики обучаемого могут не улучшаться;

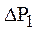- задает первый интервал изменения значений элементов вектора P(k);

k ₁ - изменяется от k до (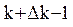), то есть второе неравенство системы в свою очередь задает систему неравенств;

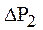- задает второй интервал изменения значений элементов вектора P(k).

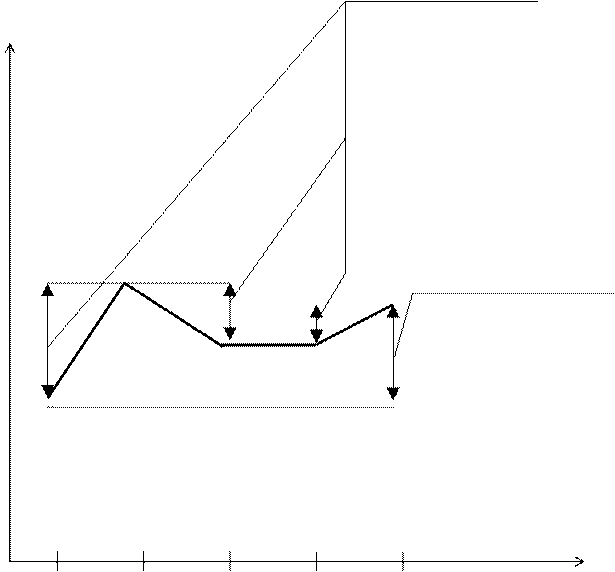
Условия аварийного окончания иллюстрируются на рис.2.1. (где ).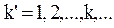

Необходимость использования системы неравенств для описания аварийного окончания вызвана тем, что моделью обучения предусматриваются ситуации, когда 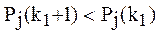, вызванные, например, забыванием (была значительная пауза в обучении), слабой мотивацией, усталостью и другими "стрессовыми" ситуациями. Эти ситуации не должны вести к аварийному окончанию.

Причиной аварийного окончания является либо слабая подготовка, либо неэффективность обучающих воздействий (комментариев к ошибкам), либо и то, и другое.

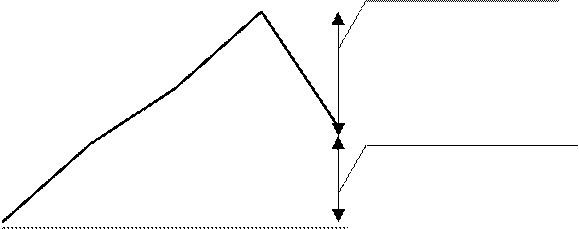
Нарушение второго неравенства системы предотвращает аварийное окончание обучения в случае, когда уровень знания обучаемого увеличивался, но произошел неожиданный спад, величина которого больше значения 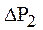("порога стресса"), и выполнилось первое неравенство системы, являющееся необходимым условием аварийного окончания (рис.2.2), где ).

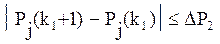
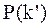
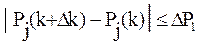
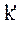
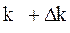
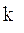
Рис. 2.1 Аварийное окончание

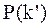
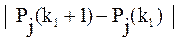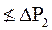
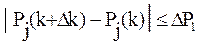
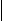
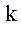
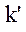
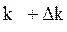
Рис. 2.2 Продолжение обучения

Идентификация знаний обучаемого.

В предлагаемой модели обучения определение 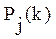осуществляется следующим образом. Для каждой операции 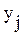вводится N гипотез 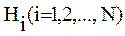, соответствующих N состояниям обученности. Каждому i-му состоянию обученности соответствует условная вероятность 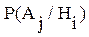правильного применения операции y _j в каждом из L _j ее применений, равная .

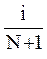Гипотезы 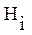образуют полную группу несовместных событий, т.е. имеет место:

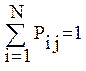(2.13)

где: P_ij- вероятность гипотезы H_i для операции y_j.

Число состояний обученности зависит от необходимой точности определения состояния обученности. Значение N задается экспертом-педагогом и используется, кроме того, для определения значения 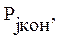, равного .

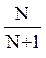На каждом шаге обучения наблюдается событие 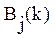, состоящее в правильном применении j-й операции 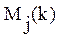раз из 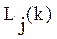заданных.

Эта информация служит для перерасчета распределения вероятностей гипотез P_ij с помощью формулы Бейеса.

Каждый k-й шаг обучения характеризуется априорным и апостериорным распределениями вероятностей гипотез о состояниях обученност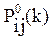и и 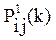, связанных между собой следующей зависимостью:

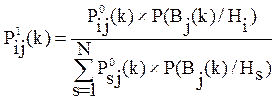(2.14)

где: 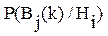- определяется по теореме Бернулли, т.е.

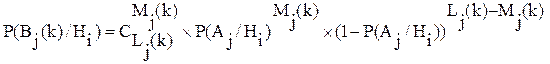(2.15)

где: 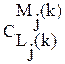- число сочетаний из 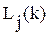по .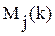

Учитывая, что априорное распределение вероятностей гипотез на k-м шаге совпадает с апостериорным распределением на (k-1)-м шаге, т.е. имеет место:

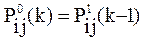(2.16)

формулу (2.14) можно переписать в виде, который подчеркивает ее рекурсивный характер (учитывается вся история обучения), а именно:

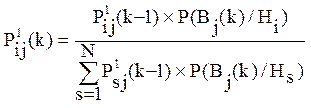(2.17)

Вероятность правильного применения операции y_j на k-м шаге определяется по формуле полной вероятности:

(2.18)

Окончательная оценка 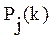получается приведением значения, вычисленного по формуле (2.18), до введенных состояний обученности.

Осуществление на k-м шаге обучения контроля ошибок и выдачи необходимых объяснений позволяет вести прогнозирование вероятности правильного применения операции y_j на (k+1)-й шаг обучения:

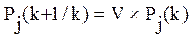(2.19)

где: V определяется следующим образом:

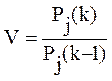(2.20)

Прогнозирование вводится после первых двух шагов обучения.

Если имеет место:

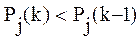(2.21)

то V приравнивается 1, так как обучающие воздействия не могут понижать уровень знаний обучаемого, тогда:

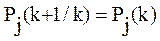(2.22)

Предложенный метод идентификации знаний обучаемого может использоваться не только при обучении навыкам алгоритмической природы, но и для других задач обучения, характеризуемых многоальтернативностью исходов шага обучения.

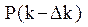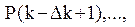
Использование бейесовского подхода при идентификации знаний, а также осуществление контроля на аварийное окончание обучения (обеспечиваемое хранением векторов , 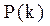для каждого текущего k) позволяет учитывать предысторию обучения при формировании очередного управляющего воздействия (учебного задания). Таким образом, создается основа для обеспечения максимальной адаптации управления процессом обучения к индивидуальным характеристикам обучаемого.

Вопросы для самоконтроля

1. Перечислите этапы которые можно выделить в каждом шаге обучения.

2. Кем разрабатывается алгоритмическое предписание?

3. Для чего служит модель обучаемого?

4. Как определяется сложность задания ?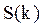

5. Когда целесообразно использование многозадачного задания?

6. В чем заключается цель обучения?

7. Когда заканчивается обучение?

8. Чем вызвана необходимость использования системы неравенств для описания аварийного окончания?

9. От чего зависит число состояний обученности?

10. Что дает использование бейесовского подхода?

Дата добавления: 2014-01-13